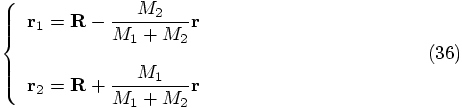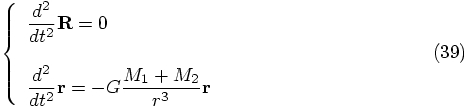4. A Gravitational 1-Body Problem
Dan: But I'm still confused. You started talking
about a change from absolute to relative coordinates. But in fact we
seem to switch from two vectors in an absolute inertial coordinate
system to two other vectors, one in the old coordinate system and one
in a new, non-inertial coordinate system. What is going on?
Erica: I guess the notation and terminology in physics is rather sloppy.
We generally don't try to be logically precise, the way mathematicians are.
But I'm glad you're forcing us to be clear about our terms. It helps
me, too, to build things up again from scratch.
It seems that there are two ways to use the notion of coordinates.
But let me first summarize what we have learned.
We have, so far, dealt with two coordinate frames. We have the
inertial one, centered on an arbitrary point, a point that is either
at rest or in uniform motion with respect to absolute space. The
coordinate axes point in fixed directions with respect to absolute
space. And we also have the non-inertial frame, centered on particle 1.
And although this frame is non-inertial, because particle 1 feels
the force of particle 2 and therefore does not move in a straight line
at constant speed, the coordinate axes of the non-inertial coordinate
system remain parallel to the coordinate axes of the inertial
coordinate system.
This last point is important. When the two particles complete one
orbit around each other, the relative vector
Now here are the two ways that physicists use `coordinates', at least
as I understand it. The first way is to give the coordinates of vectors
with respect to the coordinate frame in which they are defined. In that
case, we have already dealt with the coordinates of the four vectors
The second way to talk about coordinates is to capture the information
about a whole system, and not just a single particle with respect to
a point in space. We can say that we have described a two-body
configuration completely when we give the information contained in the
pair of vectors
So in the second way of speaking, a coordinate transformation means a
change between describing the two-body system through specifying
In the beginning of our session, I used the second way of speaking.
But then, when we started talking about coordinate systems, I guess
I slipped into the first way of speaking.
Dan: Thanks for separating those two ways of speaking. I'll have to
go over it a few times more, to get fluent in this way of thinking,
but I'm beginning to see the light.
Carol: Now the beautiful thing is: it is possible to use the
same language for both ways of speaking. This is something else I
learned in our `computer game' class as we called it, although it was
really titled as a `geometrical representation' class. If a single
vector lives in a
Mathematically speaking, each choice of a set of two vectors, whether
it is
Dan: Just when I thought I understood something, Carol manages to
make it sound all gobbledygook again. I'll just stick with Erica's
explanation.
Carol: Well, I have one question left. I mentioned that the
transformation between the
I think that is true, but I would like to prove it, to make sure, and
to see explicitly which pair of
Dan: Good questions! Erica has
shown how to derive
Erica: Yes, we can, or at least I'm pretty sure we can. But we'll have
to scratch our heads a bit to write it down. Let us start with figure
10. We can use the same figure, but now we
should consider
When I took my classical mechanics course, many homework questions
were of this type, and generally they involved a clever form of
coordinate transformation. Hmmm. Let's see. Right now the origin
is at an arbitrary point in space. We could shift to a coordinate
frame that is centered on one of our three special points; the position of
particle 1, the position of particle 2, or the position of the c.o.m.
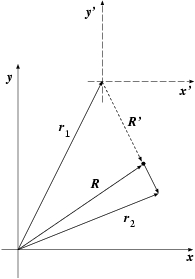
Well, why not start with particle 1, and see what happens. Let me draw
the new coordinate frame, using primed symbols:
Figure 14: A shift of coordinate frame brings the origin to the position of particle 1.
In this new frame, the c.o.m. vector is
Dan: Wait a minute, not so quick. I don't see that yet. Let me try
to take smaller steps. The vector
So far so good. And this means that we have
Carol: Elementary, my dear Watson. In the old coordinate frame, we
had Eq. (17) which gave us the position vector of the c.o.m. in
that frame. Let's write it again:
Dan: And the second particle's position is obtained simply by
interchanging the subscripts 1 and 2 everywhere, right?
Erica: Wrong, but almost right: there is an additional sign change.
We can show that in the same way as Carol just did, but putting the
origin now in the position of particle 2. Or, even simpler, we can
look at the picture, which tells us that:
Carol: First, starting with
Dan: Let me play the devil's advocate. We are doing science, so
I want to have hard evidence! As you already saw, it is all too easy
to replace a plus sign with a minus sign and stuff like that, so we'd
better make sure we really get things right. Let me try to prove it
my way.
Carol: Prove what?
Dan: Prove that we are consistent, and that we can close the circle
of transformations, from
I will take Eq. (22) and then use the original definitions
Eqs. (17) and (18):
Erica: I agree. Okay, all three of us are happy now. Let's move on!
Carol: Well, we got a new system of relative coordinates. I presume
we're going to use it for something, right?
Erica: Yes, time to rewrite Newton's equations of motion into the new system.
For the one-dimensional case above, we used Eqs. (27) in scalar
form. Let me write it in vector form. So this is the equation for the
acceleration of the first particle, due to the gravitational force
that the second particle exerts on it:
Dan: Glad to hear that! But I'm puzzled about one thing. Why is
there a third power in the denominator? I thought that
gravity shows an inverse square attraction, not an inverse cube!
And after all, that was what we wrote in Eq. (27).
Erica: Yes, the magnitude of the acceleration is indeed proportional
to the minus second power of the separation. However, we also need to
indicate the direction of the acceleration. We can define a unit
vector
Carol: I guess that Erica wrote it in the form of Eq. (27)
because it will be easier to program that way.
Erica: Indeed. Once you get used to this way of writing the equations
of motion, there is no need to introduce the new quantity
Let me also write the acceleration for the second particle:
Dan: Hmm, I'm still a bit confused about these signs. When the force
points to the first particle, why does that imply a minus sign?
Carol: The easiest way to see this is to take a particular case. Imagine
that the second particle is positioned in the origin of the coordinates.
Since gravity pulls particle 2 in the direction of particle 1, the
acceleration that particle 2 experiences points in the direction of
Dan: Ah, that is neat. Instead of trying to figure things out in
full generality, you take a particular limiting case, and check the
sign. Sort of like what Erica did, in constructing here a primed coordinate
system. Since you already know the magnitude and the line along which
the acceleration is directed, once you know the sign in one case,
you know the sign in all cases.
Carol: Yes. Technically we call this invariance under continuous
deformation. If you bring the second particle a little bit out of the
origin, by small continuous changes, the acceleration between the
particles must change continuously as well; it cannot suddenly flip
to the opposite direction.
Erica: Neat indeed: this means that understanding the sign in one
place let you know the sign in all places. I'll remember using that
trick.
Okay, onward with the equations of motion. Given Eqs.(27)
and (33), we can calculate the accelerations for the
alternative coordinates by using the defining equations (17) and
(18), as follows.
Dan: The second equation looks like a form of Newton's law of gravity,
but what does it mean that the first equation gives just zero as an answer?
Carol: Well, it seems that there is zero acceleration for the position
of the center of mass.
Dan: Ah, so the c.o.m. moves with constant velocity? But of course, that
is what we found in the one-dimensional case too.
Erica: Yes, and this means that we can choose an inertial coordinate
frame that moves along with the c.o.m., and in that coordinate frame
the center of mass does not move at all. And to make it really simple,
we can choose a coordinate frame where the c.o.m. is located at the
origin of the coordinates.
Dan: That does make life simple. In this coordinate frame, all the
information about the motions in the two-body problem is now bundled
in Eq. (35). It almost looks as if we are dealing
with a 1-body problem, instead of a 2-body problem!
Erica: Yes, this is what I meant when I announced that we could map
the two-body problem into an equivalent one-body problem, for any choice
of the masses. The original equations (27) and (33)
are coupled: both
A clear way to show this is to draw two separate figures,
Figs. 12 and 13. The c.o.m. vector
in Fig. 12 moves in a way that is totally independent of
the way the relative vector in 13 moves. The
c.o.m. vector moves at a constant speed, while the relative vector
moves as if it follows an abstract particle in a gravitational field.
To see this, notice that Eq. (35) is exactly
Newton's equation for the gravitational acceleration of a small body,
a test particle, that feels the attraction of a hypothetical body of
mass
Dan: Indeed. So the relative motion between two bodies can be described
as if it was the motion of just one body under the gravitational attraction
of another body, that happens to have a mass equal to the sum of the masses
of the two original bodies.
Erica: Exactly. And to complete this particular picture, we have to
make sure that the other body stays in the origin, at the place of the
center of mass. We can do this by giving our alternative body a mass
zero. In other words, we consider the motion of a massless test particle
under the influence of the gravitational field of a body with mass
Carol: I prefer to give it a non-zero mass. No material body can have
really zero mass. Instead, we can consider it to have just a very very
small mass. We could call it
Dan: If you like. I'm happy with the physical limit that Erica mentioned,
rather than the type of mathematical nicety that you introduced. Zero I can
understand. Because the test particle has zero mass, it exerts zero
gravitational pull on the central body. Therefore, the central body
does not move at all, and the only task we are left with is to determine
the motion of the test particle around the center.
And that is a one-body problem. Okay, I now see the whole picture.
Carol: Let us gather the formulas we have obtained so far, for our
coordinate transformation, from absolute to relative coordinates.
Erica: Yes, and let me write the equation once again here:
4.1. Coordinates
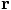 will
also complete one orbit in the non-inertial coordinate system given
in fig. 13.
will
also complete one orbit in the non-inertial coordinate system given
in fig. 13.
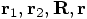 . In each case, a single vector,
or equivalently the values of the components of that vector, describe
the position of one particle with respect to a point in space. For
example,
. In each case, a single vector,
or equivalently the values of the components of that vector, describe
the position of one particle with respect to a point in space. For
example, 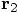 describes the position of particle 2 with
respect to the origin, and
describes the position of particle 2 with
respect to the origin, and 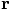 describes the position of
particle 2 with respect to the point in space temporarily occupied by
particle 1.
describes the position of
particle 2 with respect to the point in space temporarily occupied by
particle 1.
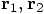 , or equivalently, in the values
of their four components in two dimensions, or their six components in
three dimensions. But we can also describe the same two-body configuration
completely by giving the information contained in the pair of vectors
, or equivalently, in the values
of their four components in two dimensions, or their six components in
three dimensions. But we can also describe the same two-body configuration
completely by giving the information contained in the pair of vectors
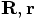 .
.
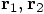 and describing the same system through
specifying
and describing the same system through
specifying 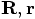 .
.
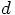 -dimensional space, then a system of
two such vectors can also be represented as a single vector in a
-dimensional space, then a system of
two such vectors can also be represented as a single vector in a
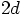 -dimensional space. And then your second way of
speaking with respect to the
-dimensional space. And then your second way of
speaking with respect to the 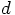 -dimensional space boils
down to your first way of speaking with respect to the
-dimensional space boils
down to your first way of speaking with respect to the
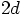 -dimensional space.
-dimensional space.
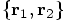 or
or 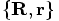 ,
determines a single point in the direct product of two copies of the
base space in which the single vectors live. In our case, we have
started from two-dimensional vectors, so the space for pairs of
vectors is four-dimensional. And the coordinate transformation that
Erica has introduced is really a bijective mapping between two
four-dimensional spaces.
,
determines a single point in the direct product of two copies of the
base space in which the single vectors live. In our case, we have
started from two-dimensional vectors, so the space for pairs of
vectors is four-dimensional. And the coordinate transformation that
Erica has introduced is really a bijective mapping between two
four-dimensional spaces.
4.2. Equivalent coordinates
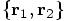 coordinate system
and the
coordinate system
and the 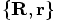 was bijective. What that means is
that any pair
was bijective. What that means is
that any pair 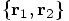 corresponds
to a unique pair
corresponds
to a unique pair 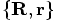 , and vice versa.
, and vice versa.
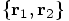 corresponds
to which pair of
corresponds
to which pair of 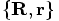 vectors.
vectors.
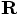 and
and 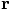 from
from
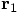 and
and 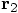 , with the definitions above.
But when we are given only
, with the definitions above.
But when we are given only 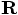 and
and 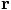 , can we
then really recover the original
, can we
then really recover the original 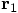 and
and 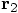 ?
?
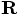 and
and 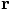 as given, and the
question is how to derive the values for
as given, and the
question is how to derive the values for 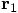 and
and
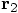 .
.
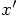 and
and
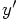 instead of
instead of 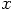 and
and 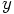 for the
coordinate axes.
for the
coordinate axes.
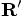 .
.
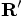 ,
pointing from the position of particle 1 to the c.o.m. This means that
we can reconstruct
,
pointing from the position of particle 1 to the c.o.m. This means that
we can reconstruct 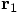 as the sum of
as the sum of 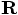 and
and
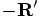 !
!
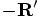 must point, by
definition, in the opposite direction of
must point, by
definition, in the opposite direction of 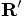 . So you can
go from the old origin to
. So you can
go from the old origin to 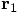 by first following the
vector
by first following the
vector 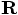 from start till tip, and then following the
vector
from start till tip, and then following the
vector 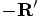 , which conveniently starts at the tip
of
, which conveniently starts at the tip
of 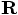 . And the tip of
. And the tip of 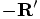 lands on particle 1.
lands on particle 1.
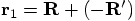 , or in simpler
terms
, or in simpler
terms

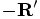 ?
?

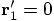 because the new origin lies smack on the first particle,
so that particle has distance zero to the new origin. And the
position vector of the second particle is given as
because the new origin lies smack on the first particle,
so that particle has distance zero to the new origin. And the
position vector of the second particle is given as
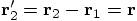 .
Erica, your choice of coordinate frame shifting was brilliant! We have
in the new frame:
.
Erica, your choice of coordinate frame shifting was brilliant! We have
in the new frame:
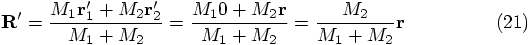
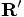 that we found in
Eq.(21), we get:
that we found in
Eq.(21), we get:

4.3. Closing the Circle
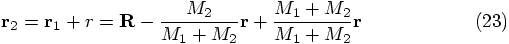

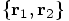 we have
derived expressions for
we have
derived expressions for 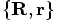 . Then, starting
with
. Then, starting
with 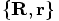 we have derived expressions for
we have derived expressions for
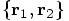 . What more could you possibly want?!?
. What more could you possibly want?!?
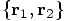 to
to
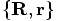 and then back again to
and then back again to 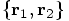 .
.
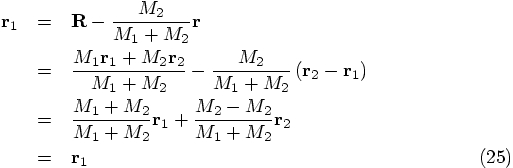
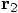 . But, to be really sure, I'd like to finish
the job:
. But, to be really sure, I'd like to finish
the job:
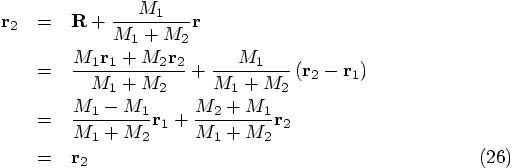
4.4. Newton's Equations of Motion


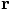 , which in our
two-dimensional case can be written as
, which in our
two-dimensional case can be written as


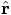 pointing in the direction of the second
particle, as seen from the position of the first particle:
pointing in the direction of the second
particle, as seen from the position of the first particle:


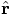 ,
since it is not used anywhere separately.
,
since it is not used anywhere separately.

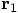 . Notice that in this particular case
. Notice that in this particular case
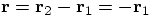 . Therefore, the direction
. Therefore, the direction
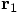 is the opposite of the direction of
is the opposite of the direction of 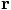 ,
hence the minus sign.
,
hence the minus sign.
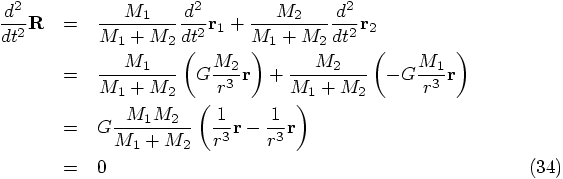
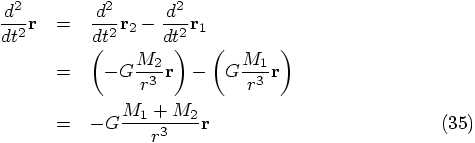
4.5. An Equivalent 1-Body Problem
 and
and  occur in both
equations, indirectly through the fact that
occur in both
equations, indirectly through the fact that  .
In contrast, the equations (34) and (35) are
decoupled.
.
In contrast, the equations (34) and (35) are
decoupled.
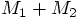 . To check this, look at Eq. (22),
and replace
. To check this, look at Eq. (22),
and replace 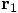 by
by 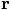 and replace
and replace
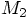 by
by 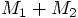 .
.
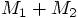 , that is located in the center of the coordinate
system.
, that is located in the center of the coordinate
system.
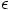 , as mathematicians do
when they talk about something so small as to be almost negligible.
, as mathematicians do
when they talk about something so small as to be almost negligible.
4.6. Wrapping Up