5. Writing the Code
Carol:
Let's start coding! Which language shall we use to write a computer code?
I bet you physics types insist on using Fortran.
Erica:
Believe it or not, most of the astrophysics code I'm familiar with has
been written in C++. It may not be exactly my favorite, but it is at
least widely available, well supported, and likely to stay with us for
decades.
Dan:
What is C++, and why the obscure name? Makes the notion of an N-body
problem seem like clarity itself!
Carol:
Long story. I don't know whether there was ever a language A, but
there certainly was a language B, which was followed alphabetically by
a newer language C, which became quite popular. Then C was extended
to a new language for object-oriented programming, something we'll
talk about later. In a nerdy pun, the increment operation ``++'' from
the C language was used to indicate that C++ was the successor
language to C.
Dan:
But everybody I know seems to be coding in Java.
Carol:
Java has a clear advantage over C++ in being almost platform independent,
but frankly, I don't like either C++ or Java. Recently, I took a
course in which the instructor used a scripting language, Ruby.
And I was surprised at the flexible way in which I could
quickly express rather complex ideas in Ruby.
Erica:
Does Ruby have something like STL?
Carol:
You mean the Standard Template Library in C++? Ruby doesn't need any
such complications because it is already dynamically typed from
the start!
Dan:
I have no idea what the two of you are talking about, but I agree with
Carol, let's start coding, in whatever language!
Carol:
We want to write a simulation code, to enable us to simulate the
behavior of stars that move under the influence of gravity. So
far we have derived the equations of motion for the relative position
of one particle with respect to the other. What we need now is an
algorithm to integrate these equations.
Dan: What does it mean to integrate an equation?
Carol: We are dealing with differential equations. In calculus,
differentiation is the opposite of integration. If you differentiate
an expression, and then integrate it again, you get the same expression
back, apart from a constant. Our differential equations describe the
time derivatives of position and velocity. In order to obtain the
actual values for the position and velocity as a function of time, we
have to integrate the differential equation.
Erica:
And to do so, we need an integration algorithm. And yes,
there is a large choice! If you pick up any book on
numerical methods, you will see that you can select from a variety of
lower-order and higher-order integrators, and for each one there are
additional choices as to the precise structure of the algorithm.
Dan:
What is the order of an algorithm?
Erica:
It signifies the rate of convergence. Since no algorithm with a
finite time step size is perfect, they all make numerical errors.
In a fourth-order algorithm, for example, this error scales as the
fourth power of the time step -- hence the name fourth order.
Carol:
If that is the case, why not take a tenth order or even a twentieth
order algorithm. By only slightly reducing the time step, we would
read machine accuracy, of order
Erica:
The drawback of using high-order integrators is two-fold: first, they
are far more complex to code; and secondly, they do not allow arbitrarily
large time steps, since their region of convergence is limited. As a
consequence, there is an optimal order for each type of problem. When
you want to integrate a relatively well-behaved system, such as the
motion of the planets in the solar system, a twelfth-order integrator
may well be optimal. Since all planets follow well-separated orbits,
there will be no sudden surprises there. But when you integrate a
star cluster, where some of the stars can come arbitrarily close to each
other, experience shows that very high order integrators lose their edge.
In practice, fourth-order integrators have been used most often for the job.
Dan:
How about starting with the lowest-order integrator we can think of?
A zeroth-order integrator would make no sense, since the error would
remain constant, independent of the time step size. So the simplest
one must be a first-order integrator.
Erica:
Indeed. And the simplest version of a first-order integrator is
called the forward Euler integrator.
Dan:
Was Euler so forward-looking, or is there also a backward Euler
algorithm?
Erica:
There is indeed. In the forward version, at each time step you simply
take a step tangential to the orbit you are on. After that, at the
next step, the new value of the acceleration forces you to slightly
change direction, and again you move for a time step
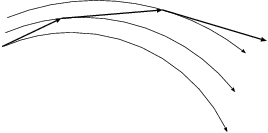
Figure 15: The forward Euler approximation is indicated by the straight arrows,
while the curved lines show the true solutions to the differential equation.
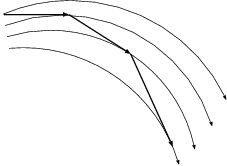
Figure 16: As figure 15, but now for the backward Euler approximation.
Carol:
Can't we do both, ie make half the mistakes of each of the two, while
trying to strike the right balance between forward and backward Euler?
Erica:
Aha! That is a good way to construct better algorithms, which then
become second-order accurate, because you have canceled the first-order
errors. Examples are second-order Runge Kutta, and leapfrog. We'll
soon come to that, but for now let's keep it simple, and stay with
first order. Here is the mathematical notation:
Carol: I have learned that in order to solve a differential equation,
you have to provide initial conditions.
Erica: Yes. It is like using a map: if you don't know where you are,
you can't use it. You start with the spot marked "you are here", and then
you can start walking, using the knowledge given by the map.
In our case, a differential equation tells you how a system evolves,
from one point to the next. Once you know where you are at time
0, the equation tells you where you will move to, and how, in
subsequent times.
So we have to specify the initial separation between the particles.
How about a simple choice like this?
Carol: Would it not be easier to use a position of
Erica: Well, as soon as we will do anything connected with the real
universe, we will have to go to 3D, so why not just start there, even
though the two-body problem is essential a 2D problem.
Dan: I don't care, either way, let's just move on. We have to translate
what Erica has just written into computer code. If it were Fortran, I would
start writing the first line as
Carol: In Ruby you do the same as in Fortran or C or C++, or Java for that
matter. In general, Ruby is designed around the `principle of least surprise.'
If you have some experience with computer languages, you will find
that whenever you encounter something new in Ruby, it is not too far
from what you might have guessed.
Erica: So assignment is exactly the same as in C?
Carol: The assignment itself is exactly the same, but there is no need to
declare anything.
Erica: Really? How does Ruby now that the variable x can hold a floating
point number and not, say, a character string or an array or whatever?
Carol: In Ruby there is no need for variable declaration, simply because
there is nothing to declare: variables have no intrinsic type. The type of
a variable is whatever you assign to it. If you write x = 3.14,
x becomes a floating point number; and if you then write x = "abs",
it becomes a string. This freedom and flexibility is expressed by saying
that Ruby is a dynamically typed language.
Erica: Isn't that dangerous?
Carol: I expected it would be, but in my experience, I in fact
made fewer mistakes using Ruby than using so-called strongly typed
languages, such as C and C++. Or stated more precisely: what mistakes
I made, I could catch far more quickly, since it would be rather
obvious if you assign pi = "abc" and then try to compute
2*pi*r and the like: you would get an error message telling
you that a string cannot be forced into a number.
Erica: so this means that we can just list the six assignments for
Carol: You can write several assignments on one line, separated
by semicolons, but I prefer to keep it simple and do it one per line.
Here they are:
By the way, does this specific choice of initial conditions mean that the
two particles will move around each other in a circle?
Erica: Probably not, unless we give exactly the right velocity
needed for circular motion. In general, the orbit will take the shape
of an ellipse, if the two particles are bound. If the initial speed
is too high, the particles escape from each other, in a parabolic or
hyperbolic orbit.
Dan: Starting from the initial conditions, we have to step forward in time.
I have no idea how large the time step step dt should be.
Carol: But at least we can argue that it should not be too large.
The distance dr over which the particles travel during a time step
dt must be very small compared to the separation between the two
particles:
Dan: In that case, we could take `much less than 1' to mean 0.1,
for starters.
Carol: I would prefer an even smaller value. Looking at fig. (15)
we see how quickly the forward Euler scheme flies off the tracks, so to speak.
How about letting `much less than 1' be 0.01? We can always make it
larger later:
Erica: We now know where we start in space, and with what velocity.
We also know the size of each time step. All we have to do is start
taking steps.
Dan: With a tiny time step of
Erica: That means we have to construct a loop. Something like `for
Carol: Let's have a look at the Ruby book. How do you repeat the same
thing k times? Ah, here it is. That looks funny! You write
k.times! So to traverse a piece of code
Dan: Surely you are joking! That is carrying the principle of least
surprise a bit too far to believe. How can that work? Can a computer
language really stay so close to English?
Carol: The key seems to be that Ruby is an object-oriented language.
Each `thing' in ruby is an object, which can have attributes such as
perhaps internal data or internal methods, which may or may not be
visible from the outside.
Dan: What is a method?
Carol: In Ruby, the word method is used for a piece of code that
can be called from another place in a longer code. In Fortran, you call
that a subroutine, while in C and C++ you call it a function. In
Ruby, it is called a method.
Erica: I have heard the term `object-oriented programming.' I really
should browse through the Ruby book, to get a bit more familiar with that
approach.
Dan: We all should. But for now, Carol, how does your key work?
Is the number
Carol: You guessed it! And every number has by default various methods
associated with it. One method happens to be called times.
Erica: And what times does is repeat the content of its argument,
whatever is within the curly brackets, k times, if the number is k.
Carol: Precisely. A bunch of expressions between curly brackets is
called a block in Ruby, and this block is executed k times. We will
have to get used to the main concepts of Ruby as we go along, but if
you want to read about Ruby in more systematic way, here is a
a good place to start, and here
is a web site specifically aimed at
scientific applications.
Dan: Amazing. Well, I would be even more amazed to see this work.
Carol: Let's test it out, using irb. This is an interactive program
that allows you to test little snippets of Ruby code. Let us explore what
it can do for us. You can invoke it simply by typing its name:
Dan: I like your prompt!
Carol: Well, I called my computer `gravity', and I set up my shell
to echo the name of my computer, so that's why it shows up here.
Dan: Quite appropriate. Now how do we interact with irb?
It seems that we can now type any Ruby expression, which will then be
evaluated right away. Let me try something simple:
Carol: Indeed. Time to test Ruby's looping construct:
Dan: ah, so c += 1 is the same as c = c + 1?
Carol: Yes. This is a construction used in C, and since taken over
by various other languages. It applies for many operators, not only
addition. For example, c *= d is the same as c = c * d.
Erica: This irb program is quite useful clearly, but I'm puzzled
about the various ways in which we can use Ruby. We are now writing
a Ruby program, by adding lines to a file, in just the same way we
would be writing a C or Fortran program, yes?
Carol: Yes and no. Yes, it looks the same, but no, it really is a
quite different approach. Ruby is an interpreted language, while C
and Fortran, and C++ as well, are all compiled languages. In Ruby,
there is no need to compile a source code file; you can just run it
directly, as we will see soon.
This, by the way, is why Ruby is called a scripting language, like
Perl and Python. In all three cases, whatever you write can be run
right away, just like a shell script. As soon as we have finished
writing our program, we will run it with the command ruby in
front of the file name, in the same way as you would run a cshell
script by typing csh filename. In our case we will type
ruby euler_try.rb.
Erica: So the difference is that in C you first compile each piece of
source code into object modules, and then you link those modules into
a single executable file, and then you run that file -- whereas in Ruby
the script itself is executable.
Carol: Exactly.
Erica: But what is the difference between typing ruby and typing
irb? If the ruby command interprets each line as it goes along,
what does irb add?
Carol: The difference is the i in irb, which stands for interactive.
In the case of irb, each line is not only interpreted, it is also
evaluated and the result is printed on the screen. In this way, you
can look into the mind of the interpreter, so to speak, and you can
follow step by step what is going on.
Dan: It sounds a bit like going into a debug mode.
Carol: I guess you could say that, yes. However, if you run a Ruby
script using the command ruby, you only get results on the screen
when you give a specific print command, such as print, as we will
see.
And just to give full disclosure, there is another hitch. If you are
starting to write a loop, say, you may have included an open parenthesis,
but not yet a closing parenthesis. In irb that is no problem; in fact,
the prompt will change, to indicate that you are one or more levels deep
inside nested expressions. But if you try to run such an incomplete file
with the ruby command, you will get an error message, even before the
Ruby interpreter starts.
Here is what happens. Upon typing ruby some-file.rb, a syntax
check is being carried out on the file some-file.rb. If the
parentheses are not balanced, a syntax error is produced, and the real
interpreter part of Ruby is not even started up.
Dan: Just like what happens in Fortran, when you get a compile error!
Carol: Yes, in a way. And to make things more confusing, many people
tend to call such an error a `compile error', even when working with
Ruby, even though in Ruby the code is not really compiled, strictly
speaking. The problem is that so-called compile errors in compiled
languages are really syntax errors; and interpreted languages can of
course have syntax errors as well. So when you hear someone telling
you `my Ruby (or Perl and Python) program didn't compile,' they mean
`my script had syntax errors.' However, strictly speaking, Ruby
initially parses the input program and transform it to a tree
structure, and then the interpreter actually traces this tree
structure, not the text string itself. So it is not entirely
incorrect to say that ruby first "compiles" a program. But this is
probably more than what you would want to know at this point.
Erica: All that is left for us to do is to write the content of the loop.
That means we have to describe how to take a single step forward in time.
Specifically, at the start we have to tell the particles how
to move to their next relative position, from our starting point of time
In addition, we have to tell the particles what their new relative velocity
using the acceleration vector
Dan: But we haven't calculated the acceleration a yet!
Carol: This is an important example of code writing, something called
`wishful thinking' or `wishful programming'. You start writing a code
as if you already have the main ingredients in hand, and then you go
back and fill in the commands needed to compute those ingredients.
Dan: That sounds like a top-down programming approach, which makes sense:
I like to start with an overview of what needs to be done. It is all too
easy to start from the bottom up, only to get lost while trying to put all
the pieces together.
Erica: To compute the acceleration, we have to solve the differential
equation for the Newtonian two-body problem, Eq. (42).
I will copy it here again:
Erica: Sure:
Carol: Let's see whether I remember my vector analysis class. The quantity
Erica: Indeed. The last quantity is a scalar because it is independent of
your choice of coordinate system. If we rotate out coordinates, the values
of
Dan: My Ruby book tells me that you must add the line
in order to use the square root method sqrt, where the term method
is used in the same way the word function is used in C and the word
subroutine is used in Fortran. The include statement is
needed to gain access to the Math module in Ruby, where
many of the mathematical methods reside.
Erica: Thanks! Now the rest is straightforward. To code up
Eq. (47), we first need to determine
Dan: Shall we see whether the program works, so far? Let's run it!
Erica: Small point, but . . . perhaps we should add a print statement,
to get the result on the screen?
Carol: I guess that doesn't hurt! The Ruby syntax for printing is
very intuitive, following the Ruby notion of the `principle of least surprise':
Erica: I like that principle! And indeed, this couldn't be simpler!
Dan: Apart from this mysterious \n at the end. What does that do?
Carol: It prints a new line. This notation is borrowed from the C language.
By the way, I'd like to see a printout of the position and velocity at the
start of the run as well, before we enter the loop, so that we get all the
points, from start to finish.
Erica: Fine! Here it is, our first program, euler_try.rb, which
is supposed to evolve our two-body problem for ten time units, from
t = 0 till t = 10:
5.1. Choosing a Computer Language
5.2. Choosing an Algorithm
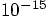for the usual double
precision (8 byte, i.e. 64 bit) representation of floating point numbers.
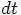in a straight line in that direction. Your approximate orbit is thus
constructed out of a number of straight line segments, where each one
has the proper direction at the beginning of the segment, but the
wrong one at the end.
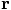and velocity 
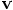of an individual particle,
where the index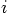 
indicates the values for time 
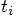and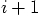 
for
the time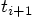 
after one more time step has been taken:
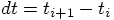. The acceleration induced on a particle by the
gravitational forces of all other particles is indicated by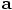 
.
So, all we have to do now is to code it up. By the way, let's rename
the file. Rather than a generic name nbody.rb, let's call it
euler.rb, or even better euler_try.rb. After all,
most likely we'll make a mistake, or two, or more, before we're finished!
5.3. Specifying Initial Conditions
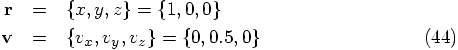
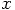axis
at a distance of one from the origin. The origin is the place where
the other particle resides, and it is the origin of the relative
coordinate system that we use. And the relative velocity is chosen to be
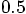in the direction of the positive 
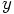axis.
This means that the initial motion is at right angles to the initial
separation.
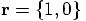and a velocity of 
,
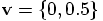in other words, to work in two dimensions?
x = 1
Erica: That is how you would do it in C or C++ as well, although you first
would have to declare the type of x, by specifying that it is a number,
in our case a floating point number, even though we initialize it here
with an integer. The meaning of the equal sign, =, can be
interpreted as follows: the value of the right-hand side of the equation
gets assigned to the variable that appears at the left-hand side. In this
case, the value of the right-hand side is already clear, it is just 1,
and after execution of this statement, the variable x has acquired the
value 1.
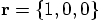and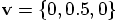 
?
Like one line for each assignment?
x = 1
y = 0
z = 0
vx = 0
vy = 0.5
vz = 0
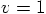and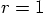 
, this means
.
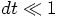5.4. Looping in Ruby
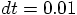, we'll have to take
at least a hundred steps to see much happening, I guess. And to go a bit
further, say from time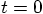 
to time 
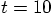, we
will need a thousand steps.
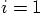till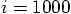 
do something.' At least that
is how most computer languages express it. I wonder how ruby does it.
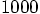times,
you enclose that piece of code within the following loop wrapper:
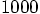also an object?
5.5. Interactive Ruby: irb
|gravity> irb
quit
and you can get out at any time by typing quit.
|gravity> irb
2 + 3
5
quit
Erica: How about going from arithmetic to algebra, by using some variables?
|gravity> irb
a = 4
4
b = 5
5
c = a * b
20
quit
I see. At the end of each line, the result of the operation is echoed.
And the value 20 is now assigned to the variable c.
|gravity> irb
c = 20
20
3.times{ c += 1 }
3
c
23
quit
Perfect! We started with 20 and three times we added 1.
5.6. Compiled vs. Interpreted vs. Interactive
5.7. One Step at a Time
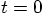to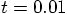 
, in our case. Or for a
general dt value, using the forward Euler approximation
(43), we obtain the position
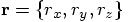at the end of the first step:
x += vx*dt
y += vy*dt
z += vz*dt
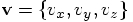should be. Using the same forward Euler construction, we can write:
vx += ax*dt
vy += ax*dt
vz += az*dt
.
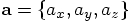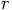is defined as
:
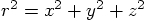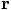is called a vector, and the quantity 
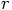is called
a scalar, right?
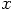and of 
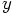and of 
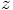may all change,
and therefore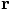 
will change. However, 
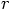will
stay the same, and that is a good thing: it denotes the physical distance
between the particles, something that you can measure. When two people use
two different coordinate systems, and both measure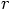 
, the value
they find had better be the same.
,
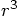and a simple way to do that is to write it as a product of two
express we have already found: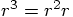 
:
r3 = r2 * sqrt(r2)
ax = - x / r3
ay = - y / r3
az = - z / r3
5.8. Printing the Result
print(x, " ", y, " ", z, " ")
print(vx, " ", vy, " ", vz, "\n")