7. Debugging the Code
Carol: This is about the simplest thing we could possibly do,
for the one-body problem: starting with a circular orbit, and then
taking only one small step. Here we go . . .
Erica: Simple, yes, but correct? Let's compute the numbers by
hand, to see whether our program gave the right answers. We start
with
Dan: That is encouraging!
Now what about the second half of the second output lines?
Erica: To compute the new velocity, we have to first compute the
acceleration vector. We can use Eq. (42), which
I'll copy here once again:
Dan: Spot on! We should have gotten
Erica: Easy to check: here is where we compute the new value of
Ooops!! A typo. How silly. No wonder we got the wrong answer for
I'm curious to see whether now everything will be all right:
Carol: Yes, we have now verified that we got the right result after
one step.
Dan: Great! Let's go back to our original code, correct the bug,
and we'll be in business.
Carol: Only if the first bug we caught will be the last bug.
Don't be so sure! We may well have made another mistake somewhere
else.
Dan: Oh, Carol, you're too pessimistic. I bet everything will be
fine now!
Erica: We'll see. Here is the same typo in euler_try.rb:
and here is the corrected program, which I will call euler.rb
in the spirit of Dan's optimism:
I'll run the new code:
Dan: No comment.
Erica: Maybe we should go back to the circular orbit. We tried to
take a single step there, and we found our typo. Perhaps we should
take a few more steps, before returning to the more general problem.
Carol: I agree. Let us sum up what we've done with our one-step code.
We have verified that our program does what the algorithm intended,
and that is certainly nice! But it is only half of the work. We
now have to check whether our particular algorithm does indeed give a
reasonable result, which corresponds to the behavior of gravitating
particles in the real world. This is called validation. In the
computer science literature these two checks are often called V&V, for
Verification and Validation.
In other words, so far in our one-step program we have passed the
verification test. The computer code does exactly what we wanted it
to do, at least for that one step. But now we have to do a validation
test.
Dan: What does that mean, concretely?
Carol: For example, we can ask whether the first step keeps the two
particles on a circular orbit. We can answer that question with pure
thought. After the first step, the new separation is:
Carol: Not bad for one step, perhaps, but our orbit has a radius of unity,
which means a circumference of
Dan: Good point. Of course, we don't know whether the errors build up
linearly, but for lack of a better idea, that would be the first guess.
Perhaps we should take an even smaller time step. What would happen
if we would use
Erica: Bravo! You have just proved that the forward Euler scheme is
a first-order scheme! Remember our discussion at the start? For a
first-order scheme, the errors scale like the first power of the time
step. You just showed that taking a time step that is ten times smaller
leads to a ten times smaller error after completing one revolution.
Dan: Great! I thought that numerical analysis was a lot harder.
Carol: Believe me, it is a lot harder for any numerical integration
scheme that is more complex than first-order. You'll see!
Dan: I can wait. For now I'm happy to work with a scheme which I can
completely understand.
Carol: So were are we. To sum up: we have verified that our
simple one-step code euler_circular_step.rb does exactly what
we want it to do. And we have validated that what we want it to do is
reasonable: for smaller and smaller time steps the orbit should stay
closer and closer to the true circular orbit.
Dan: That's the good news. But at the same time, that's also the bad
news! When we tried to integrate an arbitrary elliptical orbit, we got
a nonsense picture. How come?
Erica: We'll have to work our way up to the more complicated situation.
Let us stick to the circular orbit for now. We have a basis to start from:
the first step was correct, that we know for sure. Let's do a few more steps.
Dan: Let's try a thousand steps again.
Carol: Better to do ten steps. Each time we tried to jump forward too
quickly we've run into problems!
Erica: How about a hundred steps, as a compromise? Let's go back
to the very first code we wrote, but now for a circular orbit, and for
an integration of one time unit, which will give us a hundred steps.
Carol: Let's keep the old code, for comparison. Here is the new one.
I will call it euler_circular_100_steps.rb:
Dan: If you keep making the names longer and longer, they won't fit on
a single line anymore!
Carol: You do what you want and I do what I want; I just happen to sit
behind the keyboard.
Erica: Peace, peace! Let's not fight about names; we can later make
copies with shorter names as much as we like.
Dan: Told you so!
Carol: No, you didn't! You didn't give any reason for returning to the
old value.
Erica: Hey guys, don't get cranky. Let's just go back to
our original choice of 1,000 steps.
Carol: In that case, let's make yet another new file . . . Dan,
close your eyes, I'm adding one more
character to the file name . . . euler_circular_1000_steps.rb:
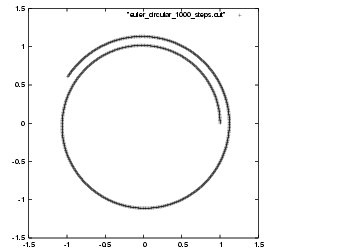
And here is our new result, which I'm calling
figure 20:
Erica: Indeed, we're really make progress.
Dan: We've come around full circle -- almost! At least the particles
are trying to orbit each other in a circle, it seems. They're just
making many small errors, that are piling up.
7.1. One Integration Step: Verification
|gravity> ruby euler_try_circular_step.rb
1 0 0 0 1 0
1.0 0.01 0.0 -0.01 0.99 0.0
Dan: . . . and getting just one short new line of output, after
the initial conditions are echoed. Nice and simple!
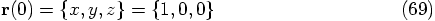
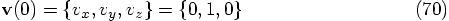
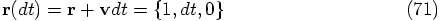
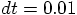 , we expect:
, we expect:
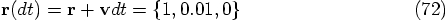

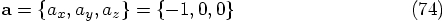
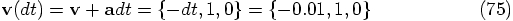
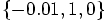 , but
we somehow wound up with
, but
we somehow wound up with 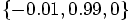 . So that's were
the bug is, in the y component of the new velocity, which should be
. So that's were
the bug is, in the y component of the new velocity, which should be
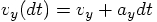 , but somehow isn't.
, but somehow isn't.
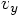 , which we call vy:
, which we call vy:
vx += ax*dt
vy += ax*dt
vz += az*dt
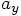 . Let me correct it right away, and write it out as
a new file, euler_circular_step.rb:
. Let me correct it right away, and write it out as
a new file, euler_circular_step.rb:
vx += ax*dt
vy += ay*dt
vz += az*dt
|gravity> ruby euler_circular_step.rb
1 0 0 0 1 0
1.0 0.01 0.0 -0.01 1.0 0.0
Dan: Wonderful! Now both the position and the velocity components
are correct, after the first step. We are winning!
7.2. A Different Surprise
vx += ax*dt
vy += ax*dt
vz += az*dt
vx += ax*dt
vy += ay*dt
vz += az*dt
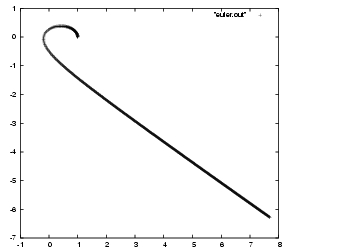
|gravity> ruby euler.rb > euler.out
And here is the plot, in fig 18:
|gravity> gnuplot
gnuplot> set size ratio -1
gnuplot> plot "euler.out"
gnuplot> quit
Carol: Well, Dan, what do you say?
7.3. One Integration Step: Validation
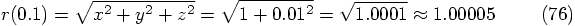
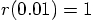 , we are half a
one hundredth of one percent off. Not bad, I would say.
, we are half a
one hundredth of one percent off. Not bad, I would say.
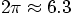 . With a velocity
of unity, it will take
. With a velocity
of unity, it will take 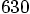 steps to go around the circle,
at the rate we are going. And if every step introduces `only' an
error of
steps to go around the circle,
at the rate we are going. And if every step introduces `only' an
error of 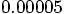 , and if the errors built up linearly, we
wind up with a total error of
, and if the errors built up linearly, we
wind up with a total error of 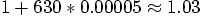 .
That is already a 3% error, even during the first revolution! And after
just a few dozen revolutions, if not earlier, the results will be meaningless.
.
That is already a 3% error, even during the first revolution! And after
just a few dozen revolutions, if not earlier, the results will be meaningless.
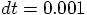 ? Let's repeat your analysis.
After one step, we would have
? Let's repeat your analysis.
After one step, we would have
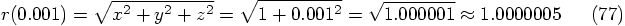
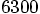 steps to go around the circle,
If the errors build up linearly, the radial separation will grow to
something like
steps to go around the circle,
If the errors build up linearly, the radial separation will grow to
something like 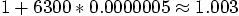 . Aha! Only
a 0.3% error, instead of 3%.
. Aha! Only
a 0.3% error, instead of 3%.
7.4. More Integration Steps
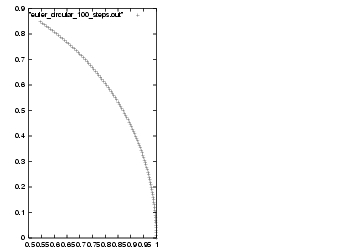
|gravity> ruby euler_circular_100_steps.rb > euler_circular_100_steps.out
Carol: Figure 19 may or may not be part of a good
circle; hard to see when you only have a small slice.
7.5. Even More Integration Steps
|gravity> ruby euler_circular_1000_steps.rb > euler_circular_1000_steps.out
Much better!