8. Convergence for a Circular Orbit
Carol: Yes, the orbit is looking recognizably circular, but that's about it.
The errors are still quite large. I would like to know exactly how
large they are. Let me have a peak at the numbers at the beginning and at
the end of the run, just like we did in the elliptic case.
Carol: Remember, just after Eq.(76),
how I estimated the error after one orbit to be 3%? After one and a third
orbit it should then have been 4%, and we got 17%. Perhaps nonlinear effects
contributed, but at least my original guess of several percent was not way
off! And I remember that Dan showed what should happen for a time step that
is ten times smaller: the error should shrink by a factor ten as
well. I'd like to test that, by changing the line:
in euler_circular_1000_steps.rb to:
and put that code in euler_circular_10000_steps.rb, to indicate that
we are now taking 1,000 steps per time unit, 10,000 time steps in total.
Time to run it!
Erica: Ah, but of course! To come back to the same place, after
making the time step ten times smaller, we have to take ten times as
many steps!
Carol: Of course indeed! Okay, I'll change the line
in euler_circular_10000_steps.rb to:
and call that file euler_circular_10000_steps_ok.rb.
Dan: Your file names are growing again without bounds, and I don't
like having so very many different files lying around.
Carol: As long as we're debugging, I'd prefer to have many files,
so that we can always backtrack to earlier versions. We can clean up
the mess later.
Dan: Okay, try again:
Carol: A 2% error, about a factor ten smaller than the 17% error
we had before. We're getting there!
Erica: And we should get a much better picture now.
Carol: Here it is, fig. 21.
Dan: Yes, the particles almost cover their own tracks, the second time
around.
Carol: You mean the particle: we're integrating a one-body problem.
Dan: Well, the distance between the two particles is what is plotted,
so I feel I can talk about particles.
Erica: And I think you're both right. Stop arguing, you guys!
Let's go back to the elliptic case, the one we started with, remember?
Carol: Sure, I remember that. All we have to do is to take
the file euler_circular.rb and make the initial velocity half
as large, by changing the line:
into:
Dan: But that will be the same file as we started with, euler.rb.
Carol: Ah, yes, of course, I had forgotten already. And in that case,
the orbit exploded.
Dan: Let's see it again. Now that we seem to understand the circular case,
perhaps we can figure out what went wrong in the elliptic case.
Carol: Okay, here we go again:
In fact, even when the steps start off with a reasonably small size at
the right hand side, by the time we have reached the left, the steps
are so large that even a circular orbit would not reach convergence if
we would everywhere use such large steps!
Dan: Why do the steps get so large, all of a sudden?
Erica: Because the particles get very close together. Notice that the
left-most part of the orbit is also the point in the orbit that is closest
to the origin, the place where
You see, we started off with a speed smaller than the speed required for
a circular orbit, in fact, we had only have of that speed. So the particles
started to fall toward each other right away, and IF we would have computed
the orbit correctly, the two particles would have returned to the
exact same spot after one revolution, just as we finally managed to
see in the circular case when we took very small steps.
Carol: So the initial position is then the place in the orbit where the
particles are furthest away from each other?
Erica: Yes, indeed! And that point is called the apocenter, from the Greek
Dan: Seeing is believing. Can you show us, Carol?
Carol: Here we go, a ten times smaller step size in
euler_elliptic_10000_steps.rb; I'll plot the result in fig.
23.
Erica: Yes, I think we're getting to the bottom of all this, finally.
Dan: But we'd better make sure, and use even smaller steps.
Carol: Will do! 8.1. Better Numbers
|gravity> ruby euler_circular_1000_steps.rb > euler_circular_1000_steps.out
|gravity> head -5 euler_circular_1000_steps.out
1 0 0 0 1 0
1.0 0.01 0.0 -0.01 1.0 0.0
0.9999 0.02 0.0 -0.0199985001874781 0.999900014998125 0.0
0.999700014998125 0.0299990001499813 0.0 -0.0299945010873182 0.999700074986127 0.0
0.999400069987252 0.0399960008998425 0.0 -0.0399870033746211 0.9994002199565 0.0
|gravity> tail -5 euler_circular_1000_steps.out
-0.967912821753728 0.639773430828751 0.0 -0.534369558098563 -0.764471400394899 0.0
-0.973256517334714 0.632128716824802 0.0 -0.528172455755398 -0.768567576556818 0.0
-0.978538241892268 0.624443041059234 0.0 -0.521945648518888 -0.772611878956261 0.0
-0.983757698377457 0.616716922269671 0.0 -0.515689587420237 -0.776604113138075 0.0
-0.988914594251659 0.608950881138291 0.0 -0.509404724445418 -0.780544088761249 0.0
Erica: The first few numbers give a distance of about 1 for the separation
of the two particles, as it should be, but the last few numbers are too large.
The separation along the x axis is about 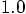 ,
and the separation along the y axis is about
,
and the separation along the y axis is about 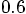 ,
and with Pythagoras that gives us a distance of
,
and with Pythagoras that gives us a distance of
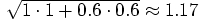 .
Not wildly off, but not very good either.
.
Not wildly off, but not very good either.
|gravity> ruby euler_circular_10000_steps.rb > euler_circular_10000_steps.out
|gravity> head -5 euler_circular_10000_steps.out
1 0 0 0 1 0
1.0 0.001 0.0 -0.001 1.0 0.0
0.999999 0.002 0.0 -0.00199999850000188 0.9999990000015 0.0
0.9999970000015 0.0029999990000015 0.0 -0.00299999450001088 0.9999970000075 0.0
0.999994000007 0.003999996000009 0.0 -0.00399998700003375 0.999994000022 0.0
|gravity> tail -5 euler_circular_10000_steps.out
0.544161847963306 0.839852844602723 0.0 -0.839087845804416 0.544480032616632 0.0
0.543322760117501 0.840397324635339 0.0 -0.839630814109985 0.54364202187099 0.0
0.542483129303391 0.84094096665721 0.0 -0.840172943245668 0.542803470813169 0.0
0.541642956360146 0.841483770128023 0.0 -0.840714232673602 0.541964380286331 0.0
0.540802242127472 0.84202573450831 0.0 -0.841254681856773 0.541124751134179 0.0
Dan: Those numbers are very different from the earlier ones . . .
8.2. Even Better Numbers
|gravity> ruby euler_circular_10000_steps_ok.rb > euler_circular_10000_steps_ok.out
|gravity> head -5 euler_circular_10000_steps_ok.out
1 0 0 0 1 0
1.0 0.001 0.0 -0.001 1.0 0.0
0.999999 0.002 0.0 -0.00199999850000188 0.9999990000015 0.0
0.9999970000015 0.0029999990000015 0.0 -0.00299999450001088 0.9999970000075 0.0
0.999994000007 0.003999996000009 0.0 -0.00399998700003375 0.999994000022 0.0
|gravity> tail -5 euler_circular_10000_steps_ok.out
-0.926888921537776 -0.42643167863865 0.0 0.411096610555956 -0.900278962470303 0.0
-0.92647782492722 -0.42733195760112 0.0 0.411969325107482 -0.899877454670898 0.0
-0.926065855602113 -0.428231835055791 0.0 0.412841644152271 -0.899475103103453 0.0
-0.925653013957961 -0.429131310158894 0.0 0.413713566877832 -0.899071908161608 0.0
-0.925239300391083 -0.430030382067056 0.0 0.414585092472074 -0.898667870239779 0.0
Dan: Great! Time for Pythagoras again:
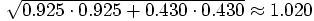 .
.
8.3. An Even Better Orbit
8.4. Reasons for Failure
|gravity> ruby euler.rb > euler.out
And here is the plot once more, in fig 22:
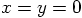 . This is called the
pericenter of an elliptic orbit. This word is derived from the Greek
. This is called the
pericenter of an elliptic orbit. This word is derived from the Greek
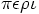 (peri) meaning `around' or `near'.
(peri) meaning `around' or `near'.
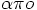 (apo) meaning `far (away) from'.
Well, I am willing to bet that a smaller time step will cure all of
our problems.
(apo) meaning `far (away) from'.
Well, I am willing to bet that a smaller time step will cure all of
our problems.
8.5. Signs of Hope
|gravity> ruby euler_elliptic_10000_steps.rb > euler_elliptic_10000_steps.out
Dan: I must admit, you may both have been right: at least now the particles
are completing a couple orbits that sort-of look elliptical, even though
the errors are still large. But at least they don't fly off to infinity
like in a slingshot.


