11. Arrays
Dan: What a difference a second-order scheme makes! Clearly, we can
the same accuracy with far fewer calculations than with a first-order
scheme. I wonder whether we can go to even higher order schemes, like
third order or fourth order or who knows what order.
Erica: Yes, in stellar dynamics, depending on the application, various
orders are used. In star cluster calculations, for example, traditionally
a fourth-order scheme has been the most popular. In contrast, in planetary
dynamics, people routine use even higher-order schemes, like tenth or twelfth
order schemes.
But before we go any further in climbing the ladder of integration orders,
I really want to write a leapfrog code. The modified Euler version
that we have discovered was interesting as such, but in astrophysics
at least, the leapfrog is used much more often. Presumably it has
some advantages, and in any case, I'd like to see how it behaves.
Dan: What is a leapfrog?
Erica: It is probably the most popular integration algorithm, not only
in astrophysics, but also in molecular dynamics, as well as in other fields.
It combines simplicity with long-term stability. Shall I sketch it out?
Carol:
Before we do your `before', I have an urgent wish: I want to clean
up the last code we've written. If we just go on adding extra lines
to produce higher-order codes, pretty soon the code becomes a bunch of
spaghetti.
Look, everything we do is spelled out separately for the x coordinate,
and the again for the y coordinate and then once again for the z
coordinate. That's just plain silly. It violates the most basic
principle in software writing, the DRY principle: Don't Repeat Yourself.
Dan: What's so wrong with repeating yourself?
Carol: Lot's of things are wrong with that! First of all, repetitions
make a code unnecessarily long, and therefore harder to read. Secondly,
if you want to modify a feature of a code, it is very difficult to do
so correctly if that same feature is repeated elsewhere in the code,
even if it is repeated in a place nearby. It is very easy to overlook
the repetition, and only modify the first instance that you encounter.
Related to that is a third point: even the first time around that you
write a code, if you start repeating yourself, it is quite likely that
you make a mistake . . .
Erica . . . as we did in our very first code, with our typo!
Carol: Yes, indeed, I'd forgotten that already. Yes, that was a classic
example of the type of penalty you can get for violating the DRY principle!
Dan: When we were drawing pictures, we could look at the vectors themselves,
but when we started coding, we had to go back to the components of the vectors.
Are you suggesting to introduce some graphical way of coding, in which we can
specify what happens directly to the vectors, as arrows, rather than to their
separate x, y, and z components?
Carol: Well, in a way. Until the middle of the previous century,
mathematicians often wrote vector equations in component form. But then
they started more and more to use vector notation, by writing down
symbols that stood for vectors as such, without any mention of components.
On the level of the mathematical equations we have written down, we have
used vector notation right from the beginning: we happily wrote things like
Carol: Yes, exactly! But for that to work, a lot more should be
understood. For example, it should also be understood that the
simple + symbol is now a much more complicated addition
operator. It should be clear to the computer that each of the
components of r1 should be added to the equivalent component
of the second expression, v1*dt. And in that last expression
the * symbol should in turn be understood to be a more
complicated multiplication operator. Multiplying a vector v1
with the scalar quantity dt should be understood as
multiplying each of the components of the vector with the same scalar.
Dan: I like the idea of simplifying the code, and making it look
more like the pen-and-paper expressions, but boy, the computer will
have to understand a lot! Let me write down what you just said, to
see whether I at least understand it.
Writing in the code a = b + c for three vector quantities
a, b, c should be translated automatically into the following
code fragment
Erica: Well, let's try to make that work. The first thing that comes
to mind is to use arrays. If we represent a vector by an array, then
each element of an array can contain a component of the vector.
Dan: That makes sense. I hope Ruby has arrays, just like Fortran?
Carol: Ruby sure does. But, as you can guess, they are far more powerful.
A single array can contain objects of different types in different elements,
and the length of an array can grow and shrink.
Dan: Seems like overkill to me. But who cares, let's get started.
Erica: Before rewriting our modified Euler code, let us start with the
simplest case, and rewrite our original forward Euler code,
euler.rb.
Carol: Here, let me translate that code, line for line, into array notation.
That way we can make sure that we perform the same calculations. Here is
file euler_array_try.rb:
As you can see, I have simply replaced x by r[0],
y by r[1], z by r[2], and similarly for the
velocities and accelerations, I have replaced vx by v[0]
and ax by a[0], and so on for the other elements.
Dan: From your example, I guess that arrays start with element zero?
Carol: Ah, yes, that's true, like in C, where the first element of an
array foo is foo[0], unlike Fortran, where the
first element is foo[1].
Erica: I noticed that right at the start of the program, you have done
a bit more already than simply replacing x = 1 by r[0] = 1,
y = 0 by r[1] = 0, and z = 0 by r[2] = 0.
Instead, you have directly assigned all three values in one line by writing
r = [1, 0, 0].
Carol: That's true too. I guess I'm getting already familiar enough
with Ruby that I had not noticed that I had made a shortcut. Yes, this
is a nice example of the compact way in which Ruby can assign values.
In fact, this line, which is the first line of the program after the
include statement, defines r as having the type `array', and in fact
an array of three elements. Similarly, the second line defines v, too,
as an array containing three elements.
In the case of r, its three elements are integers, and in the case
of v, the first and last elements are integers, and the middle
element is a floating point number. As I had mentioned before, Ruby
allows each array element to have its own dynamic type. In practice,
though, as soon as we start calculating with these numbers, most of
them will quickly become floating point numbers. Adding an integer
and a floating point number, or multiplying an integer with a floating
point number, is defined as giving a floating point number as a result,
as you would expect.
11.1. The DRY Principle
11.2. Vector Notation
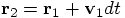 on paper, but then we tediously wrote
the same thing on our computer screen as:
on paper, but then we tediously wrote
the same thing on our computer screen as:
x2 = x1 + vx1*dt
y2 = y1 + vy1*dt
z2 = z1 + vz1*dt
Erica: So you would like to write a computer code with lines like
r2 = r1 + v1*dt
where it would be understood that r2, etc., would
be an object with the three components { x2, y2, z2 }.
ax = bx + cx
ay = by + cy
az = bz + cz
where ax is the first component of the vector a, ay is its second
component, and so on. And writing in the code a = 3*b will be
translated into
ax = 3 * bx
ay = 3 * by
az = 3 * bz
Carol: Yes, exactly. That would be nice, wouldn't it?
11.3. Arrays
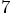 or
or
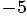 , and the class Float, which is the class of floating
point numbers, such as
, and the class Float, which is the class of floating
point numbers, such as 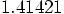 , and so on. Some classes,
such as arrays, allow objects to contain objects of other
classes. For example, the object [-5, 1.41421] is an array,
which means it is an instance of the class Array, while the two elements
are instances of the classes Fixnum and Float, respectively.
, and so on. Some classes,
such as arrays, allow objects to contain objects of other
classes. For example, the object [-5, 1.41421] is an array,
which means it is an instance of the class Array, while the two elements
are instances of the classes Fixnum and Float, respectively.