14. A Vector Class with + and -
Erica: Well, Carol, you've pulled a really neat trick. What a difference,
being able to add vectors by writing
Carol: Not quite yet; I'll have to do the same thing for subtraction,
multiplication and addition as well. And I'm sure there are a few more
things to consider, before we can claim to have a complete Vector class.
But I, too, am encouraged with the good start we've made!
I'll open a new file vector_try_add_sub.rb. First thing to add,
after addition, is subtraction. That part is easy:
Erica: So now we can write v = v1 + v2 and v = v1 - v2
But what about v = -v1? Or even just v = v1? Would that
work too?
Carol: Good question! Probably not. But before getting into the why not,
let's play with irb and see what happens:
Erica: At least writing v = v1 worked. So we've come halfway!
Dan: Ah, but would it also work if we would write v = +v1?
Let me try:
Carol: Let me consult the Ruby manual. Just a moment . . . aha, I see!
Well, this is perhaps an exception to Ruby's principle of least surprise.
The manual tells me that -@ is the Ruby notation for a
unary minus, and similarly, +@ is the Ruby notation for a
unary plus.
Dan: A unary minus?
Carol: Yes, and the word `un' in unary here means `one,' like in `unit.'
A unary minus is an operation that has only one operand.
Erica: As opposed to what?
Carol: As opposed to a binary minus. Most normal operations, such as
addition and subtraction, as well as multiplication and division, are
binary operation. Binary here means two operands. When you use a
single plus sign, you add two numbers. Similarly, a minus allows you
to subtract two numbers. So when you write 5 - 3 = 2 you are using
a binary minus. However, when you first write x = 5 and then
y = -x, to give y the value -5, you are using
not a binary minus, but a unary minus. The construction -x
returns a value that has the value of the variable x, but with
an additional minus sign.
Dan: So you are effectively multiplying x with the number
-1.
Erica: Or you could say that you are subtracting x from 0.
Carol: Yes, both statements are correct. But rather than introducing
multiplication, it is simpler to think only about subtraction. So writing
-x uses a unary minus, while writing 0-x uses a binary
minus, while both are denoting the same result.
Dan: But why does Ruby use such a complicated symbol, -@, for
unary minus?
Carol: That symbol is only used when you redefine the symbol.
Here, let me try it out, in a new file vector_try_unary.rb.
And I may as well start with the unary plus, since that seems the
simplest of the two unary operations.
We have just redefined the binary plus as follows:
We can now use the +@ symbol to redefine also the unary plus for
the same Vector class:
When we use it, we don't have to add the @ symbol, which is only
used in the definition, to make the necessary distinction between the unary
and binary plus.
Dan: That's it? You just return the vector itself? I guess it makes
sense, but it seems almost too simple. Let's try it out:
Carol: What about it?
Dan: My first guess would be to let the
method return -self but that's too simple, I'm sure . . .
Carol: Yes, that would beg the question! By writing -self
you are trying to invoke the very method you are trying to define.
That certainly won't work. But, hey, remember our friend map,
which maps an operation on all elements of an array? Well, because the
Vector class inherits the Array class, any method working for an
array will work for a vector as well, so here we go:
And here is the reality check:
Erica: Can you compose these operations arbitrarily?
Carol: Of course you can. The syntax is the same, we have only
overloaded the + and - operators; the way you
can combine them is the same as in normal arithmetic.
Erica: Let me try:
Dan: So much for normal arithmetic.
Carol: That is very unexpected, I must say. What does
the error message say? It talks about a very long array, with six
components. Wait a minute, it should only talk about vectors.
It seems that not all of our vectors are really members of the Vector
class. Could it be that some of them are still Array members?
Erica: Easy to test:
You see, self is a instance of the Vector class, which inherits
the Array class, and thereby inherits all the methods of the Array
class. But now the question is: what does a method such as map do?
It is a member of the Array class, something that Ruby folks write
as Array#map in a notation that I find somewhat confusing,
but we'll have to get used to it. So, what Array#map does,
and the only thing it can do, is to return an Array object.
Erica: And not a Vector object. Got it! So all we have to do is
to tell the result of the Array#map method to become a Vector.
But wait a minute, we can't do that. We want to pull off a little alchemy
here, turning an Array into a Vector. But doesn't this mean that the
Array class has to learn about vectors?
Carol: Well, I may have a lead here. In Ruby, you will
often see something like to_s as a method to write
something as a string. Or more precisely, to convert it into a string.
Dan: What does it mean to convert something? Can you give a really
simple example?
Carol: The simplest example I can think of is the way that integers
are being converted into floating point numbers. I'm sure you're familiar
with it. If you specify a multiplication like 3.14 * 2
to get an approximate result for
In other words, 3.14, an object that is an instance of the
class Float, will try to convert the number 2, an object that is an
instance of the class Fixnum, into an instance of the class Float.
To say it in simple terms: 3.14 will convert 2 into
2.0 and since it knows how to multiply two floating point
numbers, it can then happily go ahead and apply its multiplication
method.
Dan: I see. I guess I never worried about what happened when I
write something like 3.14 * 2; I just expect 5.28
to come out.
Carol: 6.28.
Dan: Oops, yes, of course. But you see what I mean.
Carol: I agree, normally there is no reason to think about those
things, as long as we are using predefined features that hopefully
have been tested extensively. But now we are going to define our
own objects, vectors, and we'd better make sure that we're doing
the right thing.
Erica: You mentioned the to_s method.
Carol: Yes, for each class XXX that
has a method to_s defined, as XXX#to_s, we can use
to_s to convert an object of class XXX into an object of class
String.
Here, let me show you:
So you want to do something similar with vectors, starting with an array
and then converting it into a vector, with a method like to_v.
Carol: Exactly! And I like the name you just suggested. So we have
to define a method Array.to_v. Then, once we have such a method,
we can use it to create a vector by writing
Erica: But how can we define to_v? Somebody else already has
defined the Array class for us. I guess we'll have to dig into wherever
Ruby is defined, and change the Array class definition?
Carol: No digging needed! The neat thing about Ruby, one of the neat
things, is that it allows you to augment a class. Even if someone
else had defined a class, we can always add a few lines to the class
definition, for example, when we want to add a method. The different
bits and pieces of the class definition can live in different places.
Nothing to worry about!
It should be simple. Let me copy our previous
vector_try_unary.rb into a new file vector_try.rb.
Hopefully we're getting closer to the real thing!
Here is my first attempt to augment the Array class:
And now, keeping my fingers crossed:
Dan: It may be nice, but I'm afraid I don't understand yet
how to_v works. You are returning a new vector, and that
new vector should have the same numerical components as the original
array, self, right? Now what is that little star doing there, in
front of self?
Carol: Ah, that's a way to liberate the components. We have seen
that we can create an array by writing
Now for our vector class we can similarly write:
Now, let me come back to your question. If I start with an Array
object [1, 2, 3], which internally is addressed by self,
and if I then were to write:
Carol: Indeed. And here is where the * notation comes in.
Let me show you:
Erica: So now we can go back and fix the bug in our unary minus.
Carol: Ah, yes, that's how we got started. Okay, we had in
file vector_try_unary.rb:
In our new file, vector_try.rb, I can now make this:
Dan: Shall we repeat our old trial run? Here we go:
14.1. Vector Subtraction
v = v1 + v2
rather than
v = []
v1.each_index{|k| v[k] = v1[k] + v2[k]}
Dan: Thanks, Carol! You've just made our life a whole lot easier.
|gravity> irb
require "vector_try_add_sub.rb"
true
v1 = Vector[1, 2, 3]
[1, 2, 3]
v2 = Vector[5, 6, 7]
[5, 6, 7]
v = v1 + v2
[6, 8, 10]
v = v1 - v2
[-4, -4, -4]
v = v1
[1, 2, 3]
v = -v1
NoMethodError: undefined method `-@' for [1, 2, 3]:Vector
from (irb):7
from :0
quit
Dan: Huh? A method by the name of a minus sign followed by an
@ symbol? That's the strangest method name I've ever seen.
And what can it mean that it is undefined? Should it be defined?
|gravity> irb
require "vector_try_add_sub.rb"
true
v1 = Vector[1, 2, 3]
[1, 2, 3]
v2 = Vector[5, 6, 7]
[5, 6, 7]
v = +v1
NoMethodError: undefined method `+@' for [1, 2, 3]:Vector
from (irb):4
from :0
quit
Aha! You see, we're not even half-way yet. Neither of the two work.
But it's intriguing that we get a similar error message, this time with
a plus sign in front of the mysterious @ symbol.
14.2. Unary +
def +(a)
sum = Vector.new
self.each_index{|k| sum[k] = self[k]+a[k]}
sum
end
|gravity> irb
require "vector_try_unary.rb"
true
v1 = Vector[1, 2, 3]
[1, 2, 3]
v = +v1
[1, 2, 3]
quit
Good! Now what about unary minus?
14.3. Unary -
|gravity> irb
require "vector_try_unary.rb"
true
v1 = Vector[1, 2, 3]
[1, 2, 3]
v = -v1
[-1, -2, -3]
quit
Dan: It's real. Congratulations!
|gravity> irb
require "vector_try_unary.rb"
true
v1 = Vector[1, 2, 3]
[1, 2, 3]
v2 = Vector[5, 6, 7]
[5, 6, 7]
v = -((-v1) + (+v2))
NoMethodError: undefined method `-@' for [-1, -2, -3, 5, 6, 7]:Array
from (irb):4
from :0
quit
14.4. An Unexpected Result
|gravity> irb
require "vector_try_unary.rb"
true
v1 = Vector[1, 2, 3]
[1, 2, 3]
v2 = Vector[5, 6, 7]
[5, 6, 7]
v1.class
Vector
v2.class
Vector
(+v2).class
Vector
(-v1).class
Array
quit
Carol: Aha! Unexpected, yes, but it all makes sense. For the unary
plus method, we just returned self, the object itself, which already
is a member of the Vector class. But the way I wrote the unary minus,
things are more tricky:
14.5. Converting
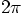 , the floating
point number 3.14 will try to make the fixed point number
2, in integer, into a floating point number first.
, the floating
point number 3.14 will try to make the fixed point number
2, in integer, into a floating point number first.
|gravity> irb
3
3
3.class
Fixnum
3.to_s
"3"
3.to_s.class
String
3.14
3.14
3.14.class
Float
3.14.to_s
"3.14"
3.14.to_s.class
String
quit
Erica: Ah, so the "..." notation already shows that we are
dealing with a character string, or string for short, and indeed, the
class of "..." is String. That makes sense.
v = [1, 2, 3].to_v
14.6. Augmenting the Array Class
class Array
def to_v
Vector[*self]
end
end
|gravity> irb
require "vector_try.rb"
true
[1, 2, 3].class
Array
[1, 2, 3].to_v.class
Vector
v1 = Vector[1, 1, 1]
[1, 1, 1]
v2 = [1, 2, 3].to_v
[1, 2, 3]
v = v1 + v2
[2, 3, 4]
v.class
Vector
quit
Erica: Your hope was justified: to_v does indeed seem
to produce genuine vectors. How nice, that we have the power to
add to the prescribed behavior of the Array class!
[1, 2, 3]
which you can view as a shorthand for
Array[1, 2, 3]
where the Array[] method receives a list of components and
returns an array that contains those components.
Vector[1, 2, 3]
in order to create vector [1, 2, 3].
Vector[self]
that would be translated into
Vector[[1, 2, 3]]
Dan: I see: that would be a vector with one component, where the
one component would be the array [1, 2, 3]. Got it. So
we have to dissolve one layer of square brackets, effectively.
|gravity> irb
a = [1, 2, 3]
[1, 2, 3]
b = [a]
[[1, 2, 3]]
c = [*a]
[1, 2, 3]
quit
14.7. Fixing the Bug
def -@
self.map{|x| -x}.to_v
end
|gravity> irb
require "vector_try.rb"
true
v1 = Vector[1, 2, 3]
[1, 2, 3]
v2 = Vector[5, 6, 7]
[5, 6, 7]
v = -((-v1) + (+v2))
[-4, -4, -4]
quit
Great! Okay, now we have really covered a complete usage of +
and - for vectors, the unary and binary forms for each of them.