16. A Matter of Speed
Dan: Clean and pretty, sure, but is it fast enough? Let's compare
the speed of the old code and the new vector code. I wonder whether
all this fancy vector stuff is affecting execution speed.
Carol: We can use the time command, to find out how much time a
code spends before finishing. We can redirect the standard output to
/dev/null, literally a null device, effectively a waste
basket. This is a Unix way of throwing the ordinary output away, the
output that appears on the standard output channel. In that way,
we are left only with output that appears on the standard error
channel, such as timing information provided by the time command.
Let me run all three forward Euler codes, the original version we wrote,
the array version, and the vector version:
Carol: Sure, here are the last lines of all three calculations:
Carol: That's a good idea. Given that our first code, euler.rb,
is rather simple, it should be easy to translate it into C. And to make
the time measurement a bit more precise, I'll make the time step a hundred
times smaller, so that we let the code make a hundred thousand steps.
Finally, we are interested now in execution speed, and for now at
least we don't worry about the cost of frequent outputs. After all,
when we switch to the real N-body problem, for
Here is the C version, for 100,000 steps, with only one output at the end,
in file euler_100000_steps.c:
Carol: Good point! Here goes:
Erica: Note that the output values differ in the last few significant
digits. That must be because optimization causes a different order of
arithmetic operations, which means that the roundoff errors are different
too. Since we are taking a hundred thousand steps, it is perhaps not
so strange that we are losing several digits in accuracy.
Dan: Time to compare these results with the Ruby code. I have this
sinking feeling that it will be muuuuuch slower.
Carol: You are probably right. Here is the simplest forward Euler version,
also with only one output statement at the end, in
euler_100000_steps.rb:
and here is the timing result:
Erica: That's a bit of a shock.
Carol: Yes, I knew that Ruby would be slow, but I didn't expect it to be
quite that slow. Well, at least C and Ruby give the same output
results, apart from the last few digits, which change anyway in C when
we switch on optimization, as we have seen. So as far as what it is the
same between the optimized and unoptimized C results, Ruby produces
that part exactly.
Dan: Let's complete the exercise and make similar versions for arrays
and vectors.
Carol: Here is the array version, in euler_array_100000_steps.rb:
and here is what timing gives:
Carol: And here is the vector version, in
euler_vector_100000_steps.rb:
and here is how slow it runs:
Carol: Let's try to get a bit more timing precision. Instead of taking
a hundred thousands steps, we can take a million steps, to make the timing
comparison more accurate. You can guess the names of the files I will
create: euler_1000000_steps.c, euler_1000000_steps.rb,
euler_array_1000000_steps.rb and
euler_vector_1000000_steps.rb.
Here are the results:
Dan: This confirms our earlier conclusions. At least on this particular
computer, that we are now using to do some speed tests, the unoptimized
C version takes 50% more time than the optimized version, the simplest
Ruby version takes about 50 times more time, the Ruby array version about
100 times more, and finally the Ruby vector version takes more than 250
times more time than the optimized C version.
Carol: But even so, for short calculations, who cares if a run takes ten
millisecond or a few seconds? I certainly like the power of Ruby in giving
us vector classes, and a lot more goodies. We have barely scratched the
surface of all the power that Ruby can give us. You should see what
we can do when we really start to pass blocks to methods and . . .
Dan: . . . and then we will start drinking a lot of coffee, while waiting
for results when we begin to run 100-body experiments! Is there no way to
speed up Ruby calculations?
Carol: There is. By the time we use 100 particles, we are talking about
Erica: I certainly like the flexibility of a high-level language like Ruby,
at least for writing a few trial versions of a new code. In order to play
around, Ruby is a lot more fun and a lot easier to use than C or C++
or Fortran. After we have constructed a general N-body code that we are
really happy with, we can always translate part of it into C, as Carol just
suggested.
Or, if really needed to gain speed, we could even translate the
whole code into C. Translating a code will always take far less time than
developing a code in the first place. And is seems pretty clear to me that
development will be faster in Ruby.
Dan: I'm not so sure about all that. In any case, we got started now
with Ruby, so let us see how far we get. But if and when we really
get bogged down by the lack of speed of Ruby, we should not hesitate
to switch to a more efficient language.
Carol: Fair enough! Let's continue our project, and apply our vector
formalism to second-order integration schemes. 16.1. Slowdown by a Factor Two
|gravity> time ruby euler.rb > /dev/null
0.053u 0.000s 0:00.05 100.0% 0+0k 0+0io 0pf+0w
|gravity> time ruby euler_array_each_def.rb > /dev/null
0.077u 0.000s 0:00.07 100.0% 0+0k 0+0io 0pf+0w
|gravity> time ruby euler_vector.rb > /dev/null
0.134u 0.001s 0:00.14 92.8% 0+0k 0+0io 0pf+0w
Dan: It seems that using our nifty vector notation, we get a penalty
in speed of a factor two. But before jumping to conclusions, can we
check once more that we are really doing the same calculations in
all three cases?
|gravity> ruby euler.rb | tail -1
7.6937453936572 -6.27772005661599 0.0 0.812206830641815 -0.574200201239989 0.0
|gravity> ruby euler_array_each_def.rb | tail -1
7.6937453936572 -6.27772005661599 0.0 0.812206830641815 -0.574200201239989 0.0
|gravity> ruby euler_vector.rb | tail -1
7.6937453936572 -6.27772005661599 0.0 0.812206830641815 -0.574200201239989 0.0
Dan: Good! And now I have another question. Presumably even the first
version is slower than an equivalent code written in Fortran or C or C++.
I would like to know how much slower.
16.2. A C Version of Forward Euler
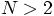 ,
the total costs will be dominated by inter-particle force calculations,
not by print statements.
,
the total costs will be dominated by inter-particle force calculations,
not by print statements.
#include <stdio.h>
#include <math.h>
int main()
{
double r[3], v[3], a[3];
double dt = 0.0001;
int ns, k;
r[0] = 1;
r[1] = 0;
r[2] = 0;
v[0] = 0;
v[1] = 0.5;
v[2] = 0;
for (ns = 0; ns < 100000; ns++){
double r2 = r[0]*r[0] + r[1]*r[1] + r[2]*r[2];
for (k = 0; k < 3; k++)
a[k] = - r[k] / (r2 * sqrt(r2));
for (k = 0; k < 3; k++){
r[k] += v[k] * dt;
v[k] += a[k] * dt;
}
}
printf("%.15g %.15g %.15g %.15g %.15g %.15g\n",
r[0], r[1], r[2], v[0], v[1], v[2]);
}
Let me compile and run it:
|gravity> gcc -o euler_100000_steps euler_100000_steps.c -lm
|gravity> time euler_100000_steps
0.292716737827072 0.382907748579753 0 -1.56551896976935 -0.313957063866527 0
0.070u 0.000s 0:00.08 87.5% 0+0k 0+0io 0pf+0w
Dan: Pretty fast indeed! But you really should compile it with the
optimizer flag -O, to bring out the real speed that C is
capable off.
|gravity> gcc -O -o euler_100000_steps euler_100000_steps.c -lm
|gravity> time euler_100000_steps
0.292716737827197 0.382907748579793 0 -1.56551896976913 -0.313957063866306 0
0.035u 0.000s 0:00.03 100.0% 0+0k 0+0io 0pf+0w
Dan: Even faster. One and a half times faster, it seems, but
we can't really be sure, given the limited accuracy of the timing output.
In any case, the C code really flies!
16.3. A Simple Ruby Version
|gravity> time ruby euler_100000_steps.rb
0.292716737826681 0.38290774857968 0.0 -1.56551896976999 -0.313957063867402 0.0
1.841u 0.003s 0:02.03 90.6% 0+0k 0+0io 0pf+0w
Dan: A dramatic difference. As far as we can see here, Ruby is at least
thirty times slower than C!
16.4. A Ruby Array Version
|gravity> time ruby euler_array_100000_steps.rb
0.292716737826681 0.38290774857968 0.0 -1.56551896976999 -0.313957063867402 0.0
3.449u 0.001s 0:05.46 63.0% 0+0k 0+0io 0pf+0w
Dan: So adding arrays let Ruby slow down by a factor two.
16.5. A Ruby Vector Version
|gravity> time ruby euler_vector_100000_steps.rb
0.292716737826681 0.38290774857968 0.0 -1.56551896976999 -0.313957063867402 0.0
9.748u 0.005s 0:10.55 92.3% 0+0k 0+0io 0pf+0w
Dan: And now we're losing yet another factor of three. That's pretty
terrible!
16.6. More Timing Precision
|gravity> gcc -o euler_1000000_steps euler_1000000_steps.c -lm
|gravity> time euler_1000000_steps
0.519970642634788 -0.376817992041735 0 1.17126787143565 0.114700879740638 0
0.456u 0.000s 0:00.48 93.7% 0+0k 0+0io 0pf+0w
|gravity> gcc -O -o euler_1000000_steps euler_1000000_steps.c -lm
|gravity> time euler_1000000_steps
0.519970642633723 -0.376817992041925 0 1.17126787143747 0.114700879739195 0
0.539u 0.000s 0:00.58 91.3% 0+0k 0+0io 0pf+0w
|gravity> time ruby euler_1000000_steps.rb
0.519970642634004 -0.376817992041834 0.0 1.17126787143698 0.114700879739653 0.0
18.212u 0.003s 0:19.81 91.9% 0+0k 0+0io 0pf+0w
|gravity> time ruby euler_array_1000000_steps.rb
0.519970642634004 -0.376817992041834 0.0 1.17126787143698 0.114700879739653 0.0
35.190u 0.015s 0:38.24 92.0% 0+0k 0+0io 0pf+0w
|gravity> time ruby euler_vector_1000000_steps.rb
0.519970642634004 -0.376817992041834 0.0 1.17126787143698 0.114700879739653 0.0
99.017u 0.022s 1:49.38 90.5% 0+0k 0+0io 0pf+0w
16.7. Conclusion
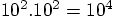 force calculations for every time step.
This means that the calculation of the mutually accelerations will take
up almost all of the computer time. What we can do is write a short C code
for computing the accelerations. It is possible to invoke such a C code
from within a Ruby code. In that way, we can leave most of the Ruby code
unchanged, while gaining most of the C speed.
force calculations for every time step.
This means that the calculation of the mutually accelerations will take
up almost all of the computer time. What we can do is write a short C code
for computing the accelerations. It is possible to invoke such a C code
from within a Ruby code. In that way, we can leave most of the Ruby code
unchanged, while gaining most of the C speed.