17. Modified Euler in Vector Form
Dan: Now that we have a vector version of forward Euler, it's time
to clean up our modified Euler code as well.
Carol: That will be an easy translation. I will start by copying
the old code from euler_modified_array.rb into a new file,
euler_modified_vector_try1.rb. All we have to do is to translate
the code from array notation to vector notation. Same as what we did
with euler_vector.rb. Here it is:
Erica: What a relief! The lines are shorter,
there are fewer lines, but what is most important: the lines are easy
to understand, with a direct correspondence between code and math.
Let's trace our history, in this regard. We started off writing with pen and
paper:
Then in our array code it became
and finally, in our vector code, we wrote:
which is very close indeed to what we started out with:
Carol: Here's the old result, from the array code:
Dan: Good! I'm happy.
Erica: But I'm not, at least not completely. Look, in the code
we are using the variable r2 in two very different ways.
Early on, we use it to hold the value of
I guess Ruby doesn't mind that we assign completely different values,
even with different types, first a scalar, then a vector. But I sure
do mind! And someone else reading our code from scratch is likely to be
confused.
Carol: You have a point there. Okay, how about calling the initial
position
and here is the test:
Erica: Yes, that's better, and you are no longer using the same
variable name for two different things. But you haven't quite done
what you said you would do, namely calling the initial position
Carol: That's because I wanted to continue using the original variables
r and v, to keep track of the evolving code. The alternative would
have been to call the running variables r0 and v0, but
that would be misleading, as if the particle would come back to the original
position each time.
Erica: How about a compromise? We can keep the original variables
r and v, but convert them to r0 and v0 at the
beginning of the loop. Let me try this, in file
euler_modified_vector_try3.rb:
and let me test it right away:
Erica: I'm not really worried about the extra two lines of code.
What's much more important is that in this new notation we can see
clearly that we have a new target of attack for the DRY principle.
Look, the two blocks of code, that I have highlighted by place blank
lines around them, are nearly identical!
Carol: Right you are! This calls for a new method. Here, let me try,
in file euler_modified_vector.rb:
and I'll test it right away:
Carol: Ah, yes. In Ruby you can return more than one value simultaneously,
and the way to do that is to list them in an array. Then, when you invoke
the method, you can just list the variables to which you want to assign the
array values, in the same order. Very lazy, very simple, and in a way, you
might say, following the principle of least surprise.
Dan: Well, yes, once you realize what is happening.
Erica: And it is quite elegant, I must say. I begin to like Ruby more and
more! The inner loop now has become almost a mathematical formula, rather
than a piece of computer code. You can read it aloud: step forward, step
again, and then average the values from the beginning and the end, both
for position and velocity, and print the results. Wonderful!
Erica: Before we move on, there is something that bothers me, which I
noticed as soon as we translated the modified Euler scheme into vector
notion, in euler_modified_vector_try1.rb. I had not noticed
any problem when we first wrote the much longer component-based version,
but when it became so compact, I realized that we are being clumsy.
Carol: How so?
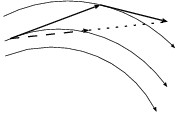
Erica: Look, we have effectively implemented figure 35,
right? Let me sketch it here again:
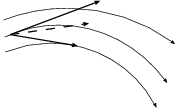
However, we started off that whole discussion, way back when, we the
simpler figure 36. Let me draw that one again too:
Carol: But you needed to compute the upper step, before you could compute
the lower step, so really both ways of drawing the picture involve two steps.
Erica: True, but to me at least the original figure suggests a somewhat
simpler procedure.
Dan: I don't care to quibble about philosophy of aesthetics.
Here is the inner loop of the first vector version that we wrote for
modified Euler:
Where do you think you can simplify things?
Erica: Let me copy that file, euler_modified_vector_try1.rb,
to euler_modified_vector_try4.rb, and let me see whether I can
change the loop, to make it look more like my understanding of the
original figure, the second one above:
Dan: That sure looks a lot simpler. Does it give the same answer?
Erica: Not only that, you can now understand the mathematical
structure better. The increments in position and velocity, in
the last two lines, are just Taylor series expansions, up to terms
that contain the accelerations. In the case of the position, the
acceleration term is second order in dt and so the original value
of the acceleration is good enough. In the case of the velocity,
we need more precision, so we take the average of the forward and
backward Euler values.
Carol: On the other hand, the inner loop in our code in
euler_modified_vector.rb was even shorter. Here it is:
Dan Yes, but at the expense of introducing an extra method, making
the whole code longer again.
Erica: I guess there is a trade off here. Introducing an extra
method gives the elegance of seeing two steps being taken explicitly,
which shortening the code as I just did brings out the Taylor series
character of the result of averaging two steps.
Carol: I agree. Well, we've learned a lot, and I am actually happy
to have several versions. In general, there is never just one right
solution for any question concerning software writing! 17.1. An Easy Translation

x1 = x + vx*dt
y1 = y + vy*dt
z1 = z + vz*dt
r1 = []
r.each_index{|k| r1[k] = r[k] + v[k]*dt}

|gravity> ruby euler_modified_array.rb | tail -1
0.400020239524913 0.343214474344616 0.0 -1.48390077762002 -0.0155803976141248 0.0
and here's what our new vector code gives:
|gravity> ruby euler_modified_vector_try1.rb | tail -1
0.400020239524913 0.343214474344616 0.0 -1.48390077762002 -0.0155803976141248 0.0
17.2. Variable Names
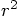 ,
the square of the original variable
,
the square of the original variable 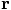 , defined as
the inner product
, defined as
the inner product
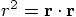 . But later, toward the end
of the loop, we use the same variable to hold value of
. But later, toward the end
of the loop, we use the same variable to hold value of
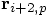 , the predicted value of
, the predicted value of 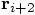 .
.
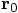 instead of
instead of 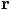 ? That is more
consistent anyway. We can then use the variable name r0
instead of r for the initial vector, and the scalar value of
its square will then become r02. So there will be no possible
confusion anymore! Here is the new listing, in file
euler_modified_vector_try2.rb:
? That is more
consistent anyway. We can then use the variable name r0
instead of r for the initial vector, and the scalar value of
its square will then become r02. So there will be no possible
confusion anymore! Here is the new listing, in file
euler_modified_vector_try2.rb:
|gravity> ruby euler_modified_vector_try2.rb | tail -1
0.400020239524913 0.343214474344616 0.0 -1.48390077762002 -0.0155803976141248 0.0
17.3. Consistency
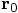 instead of
instead of 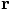 . You have only assigned
the square of
. You have only assigned
the square of 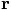 to
to 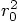 , or r02
in the code.
, or r02
in the code.
|gravity> ruby euler_modified_vector_try2.rb | tail -1
0.400020239524913 0.343214474344616 0.0 -1.48390077762002 -0.0155803976141248 0.0
Dan: Sure, that is more consistent, but you've just made the code two
lines longer! In fact, five lines longer, if you count the three blank
lines. Why did you add blank lines?
17.4. A Method Returning Multiple Values
|gravity> ruby euler_modified_vector.rb | tail -1
0.400020239524913 0.343214474344616 0.0 -1.48390077762002 -0.0155803976141248 0.0
Dan: I'm glad it works, but how does it work? It seems that your
new method step_pos_vel returns an array.
17.5. Simplification
|gravity> ruby euler_modified_vector_try4.rb | tail -1
0.400020239524793 0.34321447434461 0.0 -1.48390077762024 -0.0155803976143043 0.0
Carol: And so it does, almost. Since some of the additions and
multiplications and such are done in a different order, round-off
errors may prevent us from getting the exact same results, but this
is certainly close enough. And yes, I admit, this code is quite a
bit simpler.