20. Energy Conservation
Dan: I am glad that we now got a few second-order integration schemes.
They surely are a lot more efficient than the first-order forward Euler
scheme we started with!
Erica: Definitely. For the same amount of computer time, the
accuracy of second-order schemes is much higher. You know, it would
be nice to quantify that notion, to show exactly how accurate each
scheme really is.
Carol: We have done something like that already, by checking how the
endpoint of an orbit converged to a specific value, for smaller and
smaller time steps.
Erica: Yes, but in that case we always needed two different choices of
the time step, for two different integrations, so that we could compare
the distance between the two end points. I would prefer to use a measure
that tells us how good a single orbit calculation is. And this is indeed
what astronomers do when they compute orbits: they pick a physical quantity
that should be conversed, and they use that to get an impression of
the size of the numerical errors.
Dan: What sort of quantities do you have in mind?
Erica: The typical conserved quantities for a system of interacting
particles are energy and angular momentum. Of these, energy is a scalar
and angular momentum is a vector. Therefore, for simplicity, people
generally like to measure the change in energy, in order to get an
idea of the errors introduced during orbit integration.
Dan: Okay, let's write a method to check energy conservation.
For a system of two particles, how do you write down the total energy?
Erica: There are two contributions. There is the energy of motion,
also called kinetic energy. This energy depends only on the speed of
each particle. For a particle with mass
Dan: Why is there a minus sign?
Erica: The gravitational potential energy is normally chosen to be
zero when the two particles are very far away from each other, which
makes sense, since in that case there is almost no gravitational
interaction. Indeed, in our expression above, for
It is clear from the definition of
For example, if you place two particles at rest at a very large
distance, the kinetic energy is zero and the potential energy is
almost zero as well. Then, when the particles start falling toward
each other, the kinetic energy gets larger and larger, and therefore
more and more positive. The only way that the total energy can be
conserved is for the potential energy to become more and more negative.
Carol: In our computer programs we have used the one-body representation,
using the relative separation
Erica: Yes, we have to transform the kinetic and potential energies
from the two-body representation to the one-body representation. Let
us start with the kinetic energy. Using Eq. (93,
we get:
In our case, we have decided to use units in which
Carol: That's a bit annoying, to see that factor
In other words, whether we had equal masses,
It seems that when we want to measure energy conservation, we have to
make an extra choice, for example by specifying the ratio of the two
masses.
Dan: But the only thing we care about is whether the energy is conserved.
All we want to know whether the term between parentheses in
Eq. (101) remains constant, or almost constant.
Who cares about the funny factor in front?
Erica: Well, yes, I basically agree, but let us try to be a bit more
precise, in describing what we do. To make things clear, let me go back
to our earlier description, which still contains the total mass and the
gravitational constant. If you look at the text books, you will find
that they introduce the so-called reduced mass
Dan: Well, name or no name, let's see whether it is actually
conserved reasonably well in our calculations.
Carol: Let us start with our simplest vector code,
euler_vector.rb, and let us add some nice diagnostics.
We definitely want to check to what extent the total energy is
constant, but I would also like to see how the kinetic and potential
energy are varying.
To begin with, let me define a method energies which returns
all three energies, kinetic, potential and total, in one array:
Erica: Specific energies, that is.
Carol: Yes, but I don't feel that it is necessary to add that to
the method name.
Dan: I knew you would get tired of long names!
Carol: Only if there is no danger for confusion. In this case,
we're not going to mix specific and absolute energies -- and if we
ever do, we can always make the name longer again.
Next I would like to write a method that prints diagnostics, let me
just call it print_diagnostics, that will print out all
three energies.
Erica: But what we really need is to know the deviation from the original
energy value, to test energy conservation.
Carol: You're right. So that means that we had better measure the energy
right from the start, and then remember that value. Let us call the initial
energy e0.
Dan: That's almost too short a name, for my taste!
Carol: I was just trying to see how far I could push your taste!
Now we can use the method above, picking out the last array element
using the Array method last, to find the initial total energy
before we enter the integration loop.
Now let me think a bit carefully about the layout that
print_diagnostics should follow. We probably only need
three significant digits for the relative energy change. That
will be good enough to see how good or bad our energy conservation
is. In Ruby you can use a C like notation to fix the output format,
using expressions like printf("%.3g", x) to print the value
of a floating point variable x with three significant digits.
Actually, what I will do is use sprintf instead of printf, which
prints the same information onto a string, rather than directly onto
the output channel. That way, I can use the Ruby print command,
which takes multiple arguments. If x contains the number
Hmmm, this ought to do it. Here is the whole code:
Dan: What does STDERR mean, in front of the print statements?
Carol: That means that the information will be printed on the standard
error stream. By default, information will be printed on the standard
out stream. These are the two main output streams in Unix.
Dan: Why is it called error stream?
Carol: If you have a lot of output, you want to redirect that to a file.
But if something suddenly goes wrong, you would like to be warned about
that on the screen. You certainly don't want a warning message or error
message to be mixed in with all the other stuff in the output file; you
might never notice it there.
In our case, I would like to use this error channel to report on the
behavior of the energies. In fact, we want to determine the energy
errors, so it is somewhat appropriate to use the error stream, even
though the name suggests that it is normally used to report real errors.
But why not? We will use it here to report on small numerical errors.
Dan: So you report the values of the various energy contributions only
at the beginning and at the end of the run.
Carol: For now, that is good enough. At least it's a start. But let
me check to see whether all this works. We don't need the positions and
velocities for now, so I will redirect those to our waste basket
/dev/null
Erica: As it should be: remember, this was our very first run, when we
used a time step that was too big to integrate an elliptic orbit! We made
a huge error at pericenter. In fact, we can now see that the energy changed
sign. We started with a bound orbit, with a total energy that was negative.
But at the end of the integration the energy has become positive!
That means that the particles can escape to infinity.
Carol: Why is that?
Erica: When the particles are very far away from each other, the potential
energy becomes negligible, and the energy is dominated by the kinetic energy.
Since kinetic energy cannot be negative, such a wide separation is impossible
if the total energy is negative. But for zero or positive total energy, there
is nothing that can prevent the two particles to fly away from each other
completely. And clearly, that is what happened here, as a result of numerical
errors.
Dan: Before drawing too many conclusions, we'd better check whether we
still are talking about the same orbit as we did before.
Carol: My pleasure. Here is what the old code gave:
Erica: We know that our first orbit integration produced large errors,
and we have quantified that by looking at the final energy error, at
the end of our orbit integration. But it would be a lot more instructive
to see how the energy error is growing in time.
Carol: Easily done: in file euler_energy_try2.rb, I will modify
our print_pos_vel method to include the total energy value as well,
calling it print_pos_vel_energy instead:
As you can see, I am printing the energy last, after the positions and
velocities. And of course, in the code I'm replacing the old name by
the new name in the two invocations, just before entering the loop and
at the end of the loop. Let's run it:
Carol: That's easy to fix. In file euler_energy_try3.rb
I will change the frequent output method as follows:
This should look better now:
Carol: Let's figure out what magic incantations gnuplot wants us to
give it, to plot the energy as a function of time. To start with, let
me remember how we have plotted the orbit. Ah yes, we have been using
the fact that gnuplot use the first two columns, if you don't specify
anything otherwise. Instead of relaying on that default choice, let's
plot the orbit again, this time giving gnuplot explicit instructions to
use the data from columns 1 and 2:
Figure 43: Trajectory of our very first forward Euler integration attempt.
Now to make Carol happy, we will plot the values of the total energy,
which reside in column 7.
Dan: But wait, that is different. First we were plotting y as a function
of x. Now you are going to plot the energy E as a function of what?
Of time, I guess.
Carol: Yes, that would be the most obvious choice. And because we are
using constant time steps, that boils down to plotting E as a function
of output number, if we number the output lines successively. And indeed,
gnuplot does have a way to use the output line number as the thing to plot
along the horizontal axis: if you specify the value 0 as a column number,
the output line number will be used.
Dan: Ah, that makes sense, and that is easy to remember. If you have
an output line that reads, say, in the first three columns:
Carol: Yes, come to think of it, that must be the reason they
introduced that notation. Well, let me try:
Figure 44: Error growth for our very first forward Euler integration attempt.
Carol: Why would that be?
Erica: When the two stars come closer, the orbit becomes more curved,
and in addition, the speed becomes larger. So for both reasons, there
is more of a change in the orbit during a constant interval in time.
It would be great if we could use a smaller time step during pericenter
passage, and I'm sure we'll get to that point, later on. But for now,
as long as we are using constant time steps, a higher speed means that
each step will cover a larger distance in space. So we are in a
situation that we are actually taking longer steps in space exactly
there where the orbit is curved most.
Dan: Not a good thing to do.
Erica: I agree, but it's the simplest thing to do. We can later try
to be more clever. 20.1. Kinetic and Potential Energy
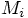and velocity
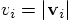, the kinetic energy is
and
, the gravitational potential energy is given by
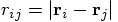is the distance between
the two particles.
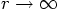you can see that
.
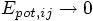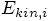that the
kinetic energy for each particle is always positive or zero. This
implies, because the total energy is conserved, that the potential
energy has to be zero or negative.
20.2. Relative Coordinates
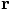and relative velocity
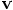, rather than the individual positions 
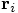and velocities 
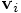of the particles. So we have to rewrite
your expressions.
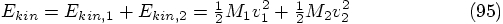
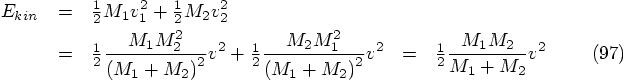
, so the last two expressions simplify to:
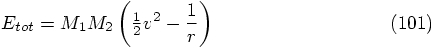
20.3. Specific Energies
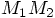coming in. So far, we did not have to specify the masses of the stars.
Our equation of motion for Newtonian gravity, Eq. (40)
contained only the sum of the masses. So when we choose that sum to
be unity, the equation became simply Eq. (42),
and we had gotten rid of any mention of masses.
,
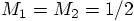whether we took one mass to be three times as large as the other,
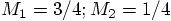, in both cases the orbits would
be exactly the same. However, you are now telling us that the total
energy will be different for those two cases. In the first case, the
factor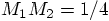 
whereas in the second case, it becomes
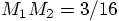, a smaller value.
,
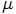defined as:
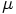, moving in the gravitational field of another
particle with mass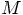 
. The total energy is given by
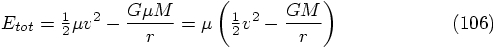
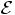as the energy per unit mass for the pseudo particle:
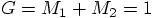, we
find for the specific total energy:
20.4. Diagnostics
def energies(r,v)
ekin = 0.5*v*v
epot = -1/sqrt(r*r)
[ekin, epot, ekin+epot]
end
, say, then writing
print "x = ", sprintf("%.3g\n", x)
gets translated into
print "x = ", "3.14\n"
and since print just concatenates its argument, this would give
the same result as typing
print "x = 3.14\n"
so you should see
x = 3.14
on the screen, where I have added the new line character \n
for good measure, to let the next prompt appear on a new line.
20.5. Checking Energy
|gravity> ruby euler_energy_try1.rb > /dev/null
E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
E_kin = 0.495, E_pot = -0.101; E_tot = 0.394
E_tot - E_init = 1.27, (E_tot - E_init) / E_init = -1.45
Dan: That does look pretty, I must say. But look, the energy is totally
different, at the beginning and at the end of the run.
|gravity> ruby euler_vector.rb > euler_vector.out
|gravity> head -1 euler_vector.out
1 0 0 0 0.5 0
|gravity> tail -1 euler_vector.out
7.6937453936572 -6.27772005661599 0.0 0.812206830641815 -0.574200201239989 0.0
And here is what the diagnostics produces, also at the very beginning and
end of the output file:
|gravity> ruby euler_energy_try1.rb > euler_energy_try1.out
E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
E_kin = 0.495, E_pot = -0.101; E_tot = 0.394
E_tot - E_init = 1.27, (E_tot - E_init) / E_init = -1.45
|gravity> head -1 euler_energy_try1.out
1 0 0 0 0.5 0
|gravity> tail -1 euler_energy_try1.out
7.6937453936572 -6.27772005661599 0.0 0.812206830641815 -0.574200201239989 0.0
Dan: Good! Exactly the same.
20.6. Error Growth
|gravity> ruby euler_energy_try2.rb > euler_energy_try2.out
E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
E_kin = 0.495, E_pot = -0.101; E_tot = 0.394
E_tot - E_init = 1.27, (E_tot - E_init) / E_init = -1.45
|gravity> head -1 euler_energy_try2.out
1 0 0 0 0.5 0 -0.0
|gravity> tail -1 euler_energy_try2.out
7.6937453936572 -6.27772005661599 0.0 0.812206830641815 -0.574200201239989 0.0 -1.45027113997184
Erica: I don't like the way these numbers are rolling on and on.
We don't really need that much precision in the positions and velocities,
if we just want to make a pretty picture. Four or five digits should be
more than enough.
|gravity> ruby euler_energy_try3.rb > euler_energy_try3.out
E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
E_kin = 0.495, E_pot = -0.101; E_tot = 0.394
E_tot - E_init = 1.27, (E_tot - E_init) / E_init = -1.45
|gravity> head -1 euler_energy_try3.out
1 0 0 0 0.5 0 -0.0
|gravity> tail -1 euler_energy_try3.out
7.6937 -6.2777 0 0.81221 -0.5742 0 -1.45027113997184
20.7. Pericenter Troubles
|gravity> gnuplot
gnuplot> set size ratio -1
gnuplot> plot "euler_energy_try3.out" using 1:2
gnuplot> quit
8 20 3
4 5 6
9 2 1
...
then it is as if gnuplot itself adds the line numbers to the left:
1 8 20 3
2 4 5 6
3 9 2 1
...
and now the column numbering starts at 0 instead of at 1.
|gravity> gnuplot
gnuplot> set size ratio -1
gnuplot> plot "euler_energy_try3.out" using 0:7
gnuplot> quit
