21. Scaling of Energy Errors
Carol: So now we have seen how we are making a really big error,
when we use forward Euler with a time step that is really too
large for a first-order integration scheme. But that's not what
we are really interested in. We want to study the behavior of
errors in the case where the time steps are small enough to give
reasonable orbit pictures.
Erica: Yes, and then we want to compare first-order and second-order
integration schemes, to check whether the energy errors scale in
different ways. First we should continue to look at forward Euler,
but with smaller time steps.
Dan: You know, I really get tired of writing a whole new file, each
time we change a parameter, like the size of a time step. Can't we
let the program ask for the time step size, so that we can type it in
while the program is running?
Carol: Good idea. That is a much cleaner approach. And while we're
at it, why not ask for the total duration of the integration too.
And that reminds me, I really wasn't very happy with the way we have
forced the code to give sparse output, at every interval of
\Delta t = 0.01.
Dan: Remind me, what did we do there?
Carol: Take file euler_elliptic_100000_steps_sparse_ok.rb
Dan: Ah, yes, of course, how can I forget such a name!
Carol: Well, as the name says, that code took 100,000 steps, during
a total time of 10 time units. With output intervals of length 0.01,
this means that we needed only 1,000 outputs. In other words, we
needed only to print the results once every 100 steps. We did this
with the following rather clumsy trick, using the remainder operator
%:
I suggest that instead we introduce the time explicitly. Notice
that so far we have used a variable dt to keep the value of the
time step size, but we have never kept track of the time itself.
Let us introduce a variable t to indicate the time that has
passed since the start of the integration. We can then specify
a desired interval between outputs, dt_out for short.
And to keep track of when the next output is scheduled to happen,
we can use a variable t_out. Whenever the time t reaches
t_out or goes past it, we need to do another output.
Of course, our diagnostics method should now print the value of the
time as well. What else do we need to change. The main loop now
becomes a test to see whether the time t has passed to or beyond
the final time t_end, specified by the user. And after each
output statement, t_out has to be incremented to the next
scheduled output time, by adding dt_out to its value.
Well, that must be about it, yes?
Let me open a file euler_energy_try4.rb and type it all in:
Dan: What is gets?
Carol: That is a Ruby input statement, short for `get string'.
It reads the next line from the command line. So if you type
a single value, and then hit the enter key, gets gobbles up
the number you have typed, but packaged as a string. For example,
when the code asks you for a time step, and you type
Erica: Let's give it the same values as before, to see whether we get
the same output.
Carol: This is what we found before:
Carol: I'll do a diff:
Erica: That last program must be taking one more step, beyond time 10.
Can you show the last few lines for both output files?
Carol: Sure:
Erica: I wonder why it overshot.
Carol: Let me put some debug statements in there, for now, just to
see what the code thinks it is doing, toward the end. Right at the
beginning of the loop, after the while line, I'll ask for the two
time values to be printed out, the running time t and the end time
t_end, in file euler_energy_try5.rb:
Here we go:
Carol: That suggests a simple solution. How about testing whether
the time has reached not exactly the end time, but close enough?
Close enough could mean half a time step. Let's try! And I'll be
bold and call the next file euler_energy.rb, in the hope
we now get it right. I will write the loop continuation test like
this:
That should do it:
Carol: Let me be double sure:
Dan: Now the point of all this was to check whether the energy errors
in forward Euler scale linearly with the time step size. Let's try a
few values.
Carol: Sure thing. And now that we can control both the time step
and the duration of the integration, let's speed things up a bit, and
integrate for only 0.1 time unit. Starting with the previous time step
we get:
Carol: Let's jump to a hundred times smaller time step, to see whether
the error still becomes a hundred times smaller:
Erica: I'd like to see how the energy error behaves in time, over a
few full orbits, and with better accuracy.
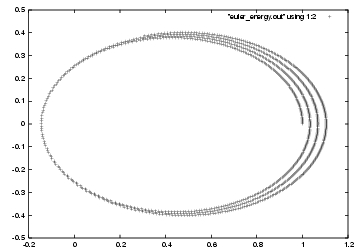
Carol: Okay, I'll take ten time units again for the total orbit
integration, and a time step of 0.0001. Just to remind us of what
the orbit looked like, I'll plot it again, in fig 45.
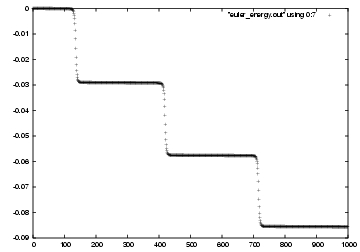
Carol: And here is how the error grows, as a function of time,
in fig 46.
Dan: Yes, dramatically so! I can see why people like to use
individual time steps. If you use thrown in a few more time steps
during close encounters, you can get very much more accuracy as a
return for investing very little extra computer time. 21.1. A Matter of Time
if i%100 == 99
print(x, " ", y, " ", z, " ")
print(vx, " ", vy, " ", vz, "\n")
end
21.2. A New Control Structure
0.01
then gets returns the string "0.01", made up of four characters.
What we really want is a number, and the method to_f is the
built-in Ruby way to convert a string into a floating point number;
it is short for `(convert) to float'.
21.3. Overshooting
|gravity> ruby euler_energy_try3.rb > euler_energy_try3.out
E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
E_kin = 0.495, E_pot = -0.101; E_tot = 0.394
E_tot - E_init = 1.27, (E_tot - E_init) / E_init = -1.45
And let us see what our new program gives:
|gravity> ruby euler_energy_try4.rb > euler_energy_try4.out
time step = ?
0.01
final time = ?
10
t = 0, E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
t = 10, E_kin = 0.495, E_pot = -0.101; E_tot = 0.394
E_tot - E_init = 1.27, (E_tot - E_init) / E_init = -1.45
Dan: At least the diagnostics output is the same. How about the
output files?
|gravity> diff euler_energy_try3.out euler_energy_try4.out
1001a1002
> 7.7019 -6.2835 0 0.81213 -0.57414 0 -1.45027103130336
He, that is strange. Our friend diff claims that the two files
are identical except for the fact that our latest code produces one
more line of output! Let me check it with a word count:
|gravity> wc euler_energy_try[34].out
1001 7007 59973 euler_energy_try3.out
1002 7014 60033 euler_energy_try4.out
2003 14021 120006 ¹ç·×
And what do you know, yes, 1001 lines in euler_energy_try3.out
as it should be, moving from times 0 till 10 with steps of 0.01, but
why does euler_energy_try4.out have 1002 lines??
|gravity> tail -3 euler_energy_try3.out
7.6775 -6.2662 0 0.81236 -0.57433 0 -1.45027135833743
7.6856 -6.272 0 0.81229 -0.57426 0 -1.45027124898271
7.6937 -6.2777 0 0.81221 -0.5742 0 -1.45027113997184
|gravity> tail -3 euler_energy_try4.out
7.6856 -6.272 0 0.81229 -0.57426 0 -1.45027124898271
7.6937 -6.2777 0 0.81221 -0.5742 0 -1.45027113997184
7.7019 -6.2835 0 0.81213 -0.57414 0 -1.45027103130336
Just like diff told us, the last few lines are identical, except for
the fact that euler_energy_try4.out shows one extra step. You
must be right: it looks like the code didn't know how to stop in time.
21.4. Knowing When To Stop
while t < t_end
print "t = ", t, " and t_end = ", t_end, "\n"
|gravity> ruby euler_energy_try5.rb > euler_energy_try5.out
time step = ?
0.01
final time = ?
10
t = 0, E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
t = 10, E_kin = 0.495, E_pot = -0.101; E_tot = 0.394
E_tot - E_init = 1.27, (E_tot - E_init) / E_init = -1.45
|gravity> tail euler_energy_try5.out
t = 9.95999999999983 and t_end = 10.0
7.6694 -6.2605 0 0.81244 -0.57439 0 -1.45027146803748
t = 9.96999999999983 and t_end = 10.0
7.6775 -6.2662 0 0.81236 -0.57433 0 -1.45027135833743
t = 9.97999999999983 and t_end = 10.0
7.6856 -6.272 0 0.81229 -0.57426 0 -1.45027124898271
t = 9.98999999999983 and t_end = 10.0
7.6937 -6.2777 0 0.81221 -0.5742 0 -1.45027113997184
t = 9.99999999999983 and t_end = 10.0
7.7019 -6.2835 0 0.81213 -0.57414 0 -1.45027103130336
Erica: Aha! The problem is roundoff, that explains everything!
The time variable t is a floating point variable, and instead
of reaching the exact time 10, after 1,000 steps, it comes ever
so close, but not quite at the right point. Therefore, when it
runs the loop test, it decides that the time has to be incremented
by another time step, and it then overshoots.
|gravity> ruby euler_energy.rb > euler_energy.out
time step = ?
0.01
final time = ?
10
t = 0, E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
t = 10, E_kin = 0.495, E_pot = -0.101; E_tot = 0.394
E_tot - E_init = 1.27, (E_tot - E_init) / E_init = -1.45
|gravity> diff euler_energy_try3.out euler_energy.out
Dan: And it did it. No differences. Congratulations!
|gravity> tail -1 euler_energy_try3.out
7.6937 -6.2777 0 0.81221 -0.5742 0 -1.45027113997184
|gravity> tail -1 euler_energy.out
7.6937 -6.2777 0 0.81221 -0.5742 0 -1.45027113997184
Good. So now we have a new tool, allowing us to change two parameters,
without having to change the source code each time. Progress!
21.5. Linear Scaling
|gravity> ruby euler_energy.rb > euler_energy.out
time step = ?
0.01
final time = ?
0.1
t = 0, E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
t = 0.1, E_kin = 0.129, E_pot = -1; E_tot = -0.874
E_tot - E_init = 0.000626, (E_tot - E_init) / E_init = -0.000715
Making the time step ten times shorter, we find:
|gravity> ruby euler_energy.rb > euler_energy.out
time step = ?
0.001
final time = ?
0.1
t = 0, E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
t = 0.1, E_kin = 0.129, E_pot = -1; E_tot = -0.875
E_tot - E_init = 6.26e-05, (E_tot - E_init) / E_init = -7.16e-05
And making it yet ten times shorter gives:
|gravity> ruby euler_energy.rb > euler_energy.out
time step = ?
0.0001
final time = ?
0.1
t = 0, E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
t = 0.1, E_kin = 0.129, E_pot = -1; E_tot = -0.875
E_tot - E_init = 6.26e-06, (E_tot - E_init) / E_init = -7.16e-06
Dan: Pretty linear, all right.
|gravity> ruby euler_energy.rb > euler_energy.out
time step = ?
0.000001
final time = ?
0.1
t = 0, E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
t = 0.1, E_kin = 0.129, E_pot = -1; E_tot = -0.875
E_tot - E_init = 6.26e-08, (E_tot - E_init) / E_init = -7.16e-08
Dan: And so it does.
21.6. Picture Time
|gravity> ruby euler_energy.rb > euler_energy.out
time step = ?
0.0001
final time = ?
10
t = 0, E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
t = 10, E_kin = 1.27, E_pot = -2.07; E_tot = -0.8
E_tot - E_init = 0.0749, (E_tot - E_init) / E_init = -0.0856
Erica: Ah, yes, that time step was just about short enough to begin
to see the intended orbit, without too much drift.
 .
.
 .
.