22. Error Scaling for 2nd-Order Schemes
Dan: Let's have a look at our second-order integration schemes.
If I understand things correctly, they are supposed to improve
energy quadratically, right? When we make the time step ten times
smaller, the energy error should become one hundred times smaller.
Carol: That's the expectation, yes. But first I have to write the
codes. I will start with the modified Euler algorithm, for which we
had written the vector version of the code in file
euler_modified_vector.rb. I will open a new file
euler_modified_energy.rb, and add the same type of energy
output statements and diagnostics as we have done for the forward
Euler case. Here we go:
Dan: That all looks pretty straightforward.
Carol: And now it is just a matter of making the time steps
smaller and smaller:
Carol: Well, yes, with double precision you can't get much further
than
Dan: But wait, just one thing: we haven't checked yet whether we
are still getting the same results as before.
Carol: Ah, yes, safety first! The old code gave:
Carol: Finally, time to let the leapfrog algorithm tell us whether
it is really a second-order algorithm as well. I will start with
leapfrog.rb. I will open a new file
leapfrog_energy.rb, and again I will add the same type
of energy output statements and diagnostics. Here it is:
Carol: I'll just use the same parameters as I did while testing the
modified Euler scheme, for making the time steps smaller and smaller:
Erica: An amazing accuracy, and that after 100,000 steps! What
happened? I would have thought that the cumulative effects of
100,000 roundoff errors would have spoiled the fun.
Carol: We were probably just lucky in the way the roundoff errors
canceled. Notice that the energy error at first got 100 times smaller,
each time we made the time step 10 times smaller, as it should for a
second-order algorithm. But in the last round, the improvement was a
lot less than a factor 100.
We must be really close to the roundoff barrier now. Let me just make
the time step a factor two smaller. That should make the total error
grow again. Wanna bet?
Dan: No, but I do wanna see whether you're right.
Carol: Here we go;
Carol: I must say, I'm surprised that the roundoff errors cancel so well.
But this just can't go on. If shrink the time step factor by another factor
of two.
Dan: But you didn't feel confident enough to ask us to bet, this time.
Carol: I should have! And yes, before you ask me, let us check whether
we still get the same output as before. What we got was:
22.1. Modified Euler
22.2. Energy Error Scaling
|gravity> ruby euler_modified_energy.rb > /dev/null
time step = ?
0.01
final time = ?
0.1
t = 0, E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
t = 0.1, E_kin = 0.129, E_pot = -1; E_tot = -0.875
E_tot - E_init = -8.33e-08, (E_tot - E_init) / E_init = 9.52e-08
|gravity> ruby euler_modified_energy.rb > /dev/null
time step = ?
0.001
final time = ?
0.1
t = 0, E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
t = 0.1, E_kin = 0.129, E_pot = -1; E_tot = -0.875
E_tot - E_init = -7.19e-10, (E_tot - E_init) / E_init = 8.22e-10
|gravity> ruby euler_modified_energy.rb > /dev/null
time step = ?
0.0001
final time = ?
0.1
t = 0, E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
t = 0.1, E_kin = 0.129, E_pot = -1; E_tot = -0.875
E_tot - E_init = -7.07e-12, (E_tot - E_init) / E_init = 8.08e-12
|gravity> ruby euler_modified_energy.rb > /dev/null
time step = ?
0.00001
final time = ?
0.1
t = 0, E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
t = 0.1, E_kin = 0.129, E_pot = -1; E_tot = -0.875
E_tot - E_init = -4.25e-14, (E_tot - E_init) / E_init = 4.86e-14
|gravity> ruby euler_modified_energy.rb > /dev/null
time step = ?
0.000001
final time = ?
0.1
t = 0, E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
t = 0.1, E_kin = 0.129, E_pot = -1; E_tot = -0.875
E_tot - E_init = -1.41e-13, (E_tot - E_init) / E_init = 1.61e-13
Erica: Up till the last run, it looked almost too good to be true.
We must have hit roundoff, I guess.
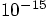 in relative accuracy for a single
calculation. I'm surprised we got as close as we did. Most of the
roundoff errors must have cancelled, in the 10,000 steps we took in
the next to last integration. But in the last run, where we took
100,000 steps, we accumulated more roundoff errors. When you are
adding more steps, you'll get more roundoff, no matter how accurate
each individual step may be.
in relative accuracy for a single
calculation. I'm surprised we got as close as we did. Most of the
roundoff errors must have cancelled, in the 10,000 steps we took in
the next to last integration. But in the last run, where we took
100,000 steps, we accumulated more roundoff errors. When you are
adding more steps, you'll get more roundoff, no matter how accurate
each individual step may be.
|gravity> ruby euler_modified_vector.rb | tail -1
0.400020239524913 0.343214474344616 0.0 -1.48390077762002 -0.0155803976141248 0.0
and we should get the same result for our new code, if we give it
the same parameters:
|gravity> ruby euler_modified_energy.rb | tail -1
0.400020239524913 0.343214474344616 0.0 -1.48390077762002 -0.0155803976141248 0.0
Dan: All is well.
22.3. Leapfrog
22.4. Another Error Scaling Exercise
|gravity> ruby leapfrog_energy.rb > /dev/null
time step = ?
0.01
final time = ?
0.1
t = 0, E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
t = 0.1, E_kin = 0.129, E_pot = -1; E_tot = -0.875
E_tot - E_init = 1.19e-07, (E_tot - E_init) / E_init = -1.36e-07
|gravity> ruby leapfrog_energy.rb > /dev/null
time step = ?
0.001
final time = ?
0.1
t = 0, E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
t = 0.1, E_kin = 0.129, E_pot = -1; E_tot = -0.875
E_tot - E_init = 1.19e-09, (E_tot - E_init) / E_init = -1.36e-09
|gravity> ruby leapfrog_energy.rb > /dev/null
time step = ?
0.0001
final time = ?
0.1
t = 0, E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
t = 0.1, E_kin = 0.129, E_pot = -1; E_tot = -0.875
E_tot - E_init = 1.19e-11, (E_tot - E_init) / E_init = -1.36e-11
|gravity> ruby leapfrog_energy.rb > /dev/null
time step = ?
0.00001
final time = ?
0.1
t = 0, E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
t = 0.1, E_kin = 0.129, E_pot = -1; E_tot = -0.875
E_tot - E_init = 1.15e-13, (E_tot - E_init) / E_init = -1.31e-13
|gravity> ruby leapfrog_energy.rb > /dev/null
time step = ?
0.000001
final time = ?
0.1
t = 0, E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
t = 0.1, E_kin = 0.129, E_pot = -1; E_tot = -0.875
E_tot - E_init = -6.22e-15, (E_tot - E_init) / E_init = 7.11e-15
22.5. Roundoff Kicks In
|gravity> ruby leapfrog_energy.rb > /dev/null
time step = ?
0.0000005
final time = ?
0.1
t = 0, E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
t = 0.1, E_kin = 0.129, E_pot = -1; E_tot = -0.875
E_tot - E_init = 4.66e-15, (E_tot - E_init) / E_init = -5.33e-15
Dan: I should have accepted your challenge, and made a bet against you!
|gravity> ruby leapfrog_energy.rb > /dev/null
time step = ?
0.00000025
final time = ?
0.1
t = 0, E_kin = 0.125, E_pot = -1; E_tot = -0.875
E_tot - E_init = 0, (E_tot - E_init) / E_init = -0
t = 0.1, E_kin = 0.129, E_pot = -1; E_tot = -0.875
E_tot - E_init = -2.74e-14, (E_tot - E_init) / E_init = 3.13e-14
So there! Now the errors are finally accumulating enough to show a worse
performance.
|gravity> ruby leapfrog.rb | tail -1
0.583527377458303 -0.387366076048216 0.0 1.03799194001953 0.167802127213742 0.0
And what our new code gives is:
|gravity> ruby leapfrog_energy.rb | tail -1
0.583527377458303 -0.387366076048216 0.0 1.03799194001953 0.167802127213742 0.0
Good.