3. Finding Binaries
Alice: A job well done! Now every ruby program that starts with
require "acs" will automatically receive options for specifying
precision, indentation, and verbosity levels for reporting diagnostics
on the standard error channel as well as in the stories that appear on
the standard output channel.
Bob: I'm glad we have all that in place. Now, finally let's get back
to our task: letting some real physics come out! We've been talking about
determining the time of first binary formation.
In order to do so, we have to recognize binaries when they are formed.
Well, I added a quick-and-dirty binary finding part to the diagnostics
of our individual time step integrator. I started with world3.rb,
but I'm calling it world4.rb now, with that addition.
At the top of world4.rb, I'm including a file,
binary.rb, that contains a new class Binary. Here it is:
Alice: I see. You create a new instance of the Binary class by giving
it two bodies. The initializer then immediately determines the relative
position and velocity as well as the total mass and the reduced mass.
From that point on, you can ask the binary what its eccentricity or
semi-major axis is, or its period, or some other piece of information.
In each case, the answer is provided through a call to a method within the
Binary class, where the method computes the answer on the fly.
Bob: Indeed. I could have done a more complete job, by adding information
about all six orbital elements, preferably in various coordinate systems.
For now, though, the main information we are interested in is the hardness
of the binary, its internal energy.
Alice: Which you call rel_energy to indicate that it is the energy
in the relative motion of the two stars, independent of the energy in the
center-of-mass motion of the binary. And you provide the semi-major axis
because that is directly related to the internal energy.
Bob: Yes, the semi-major axis a is inversely proportional to the binary
binding energy rel_energy, for given values of the two masses.
And once I had computed a I thought I might as well also compute e,
the eccentricity of the orbit, which has a simple relation with the
relative angular momentum, as you can see in the binary.rb listing.
Alice: Now how did you use this class to report binary diagnostics within
the integrator?
Bob: In world4.rbo, in the class WorldEra, I have added
the following method:
Alice: So this method takes a snapshot at the requested time, asks the
snapshot to return the binary diagnostics, and then reports that information
with our new acs_log function.
Bob: I could of course have given the value 1 directly to the first argument
of acs_log, but I prefered to keep it a free variable, v, which
is easier to notice and to chance later, if so desired. For the time being,
it will have the value 1, which means a verbosity level of 1.
Alice: Let me see whether I got all this correctly now. If the user invokes
the integrator with
Bob: That is indeed correct. And I must say, I'm really glad to have such
a versatile and general tool for direction information where it is
needed!
Alice: Let me look how you have implemented the real work, in the
binary_diagnostics method within the WorldSnapshot class:
As before, you introduce the variable v right at the start and set it
equal to 1, which is the normal verbosity level. And then in the third
line you introduce a measure of precision, prec.
Bob: Yes. I could have used the normal precision specified in our
standard ACS precision, which by default is 16 digits long for floating
point variables. However, it would be destracting to list the semimajor
axis of a binary in full double precision. Therefore I introduced a
special command line option to describe the binary diagnostics precision.
Here, you can find it among the ever growing list of options for
world4.rb :
Bob: This is of course rather wastful of computer time, and not very
efficient. If we would be dealing with tens of thousands of
particles, we may want to think of a more clever scheme. But for now,
this seems like the simplest way of doing things.
Alice: I agree. Premature optimization is the root of all evil, as we
already said! So for each pair you first check whether it is bound. Only
if the relative energy is negative do you continue and check the semi-major
axis. And only if that value is smaller than the maximum value allowed,
do you print diagnostics information.
Bob: Well, sprint diagnostics information, you mean; the information is
printed on a string, and the string is passed back to the calling function.
Alice: And that calling function, also named binary_diagnostics
within the WorldEra class, can use that string both for printing on the
standard error stream and for adding it to the total ACS wrapped output on
the standard output stream. Got ya! And in the list of options above
I already saw how the user can set the maximum semi-major axis value.
Great! It all seems to be quite transparent. Last question: how and where
does the WorldEra#binary_diagnostics method get invoked? Most
likely on the World level, and close to the other diagnostics. But I
don't see the word binary in the listing of clas World.
Bob: Almost correct. You are right in that the calls indeed follow the
calls to the WorldEra#write_diagnostics methods, literally
so, but they occur in the module Output. But then the module
Output gets mixed into the class World, so a language lawyer might
argue that the calls occur at the World level. Hera are the two
places where it happens, first for normal diagnostics output:
and then for unscheduled diagnostics output, when a CPU limit is
reached before a whole era is finished:
Alice: No need for lawyers here; I think I was close enough. Now I'd
like to see your binary diagnostics in actions. How shall I begin?
Bob: Easy enough, why not just do what the programs suggest you do,
when you use the ---help option.
Alice: I keep forgetting that we have such a nice way to do the
hand-holding, for users and developers alike! Here we are:
Bob: I bet that's more than you wanted!
Alice: Yeah, I have to learn to tame our programs. But it is nice to
see the same diagnostics appearing on the screen and within the story
that now appears within the ACS wrapped particle output.
Let me exercise your new options. I will ask only for binaries that
have a semimajor axis smaller than 0.5, and I want to know the results
only to the first two significant digits. And I certainly don't want
all that output. I could redirect it to /dev/null, but let
me instead set the time of next output to, say, 1000, to make sure that
we don't see it within our run. Here goes:
3.1. A Binary Class
3.2. Verbosity
def binary_diagnostics(t)
v = 1
acs_log(v, take_snapshot(t).binary_diagnostics)
end
kali world4.rb --verbosity 0 --acs_verbosity 2
no binary diagnostics will appear on the standard error stream, but it
will be written in the story of WorldEra. Similarly, running
the code as
kali world4.rb --verbosity 1 --acs_verbosity 0
will show binary diagnostics will on the standard error stream, but will
not write anything in the stories that appear on the standard output stream.
In general,
kali world4.rb --verbosity v1 --acs_verbosity v2
will only show diagnostics information on the screen when 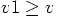 and will only add the information to the WorldEra story when
and will only add the information to the WorldEra story when
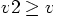 , where
, where 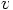 is the first argument of
acs_log.
is the first argument of
acs_log.
3.3. The WorldSnapshot Level
|gravity> kali world4.rb -h
Individual Time Step, Individual Integration Scheme Code
-g --integration_method: Choice of integration method [default: hermite]
-c --step_size_control : Determines the time step size [default: 0.01]
-f --init_timescale_factor: Initial timescale factor [default: 0.01]
-e --era_length : Duration of an era [default: 0.0078125]
-m --max_timestep_param: Maximum time step (units dt_era) [default: 1]
-d --diagnostics_interval: Diagnostics output interval [default: 1]
-o --output_interval : Snapshot output interval [default: 1]
-y --pruned_dump : Prune Factor [default: 0]
-t --time_period : Duration of the integration [default: 10]
-u --cpu_time_max : Max cputime diagnost. interval [default: 60]
-i --init_out : Output the initial snapshot
-r --world_output : World output format, instead of snapshot
-a --shared_timesteps : All particles share the same time step
-x --max_semi_major_axis: Maximum semi-major axis [default: 1.0e+30]
--binary_diag_precision : Binary Diagnostics Precision [default: 4]
--verbosity : Screen Output Verbosity Level [default: 1]
--acs_verbosity : ACS Output Verbosity Level [default: 1]
--precision : Floating point precision [default: 16]
--indentation : Incremental indentation [default: 2]
-h --help : Help facility
---help : Program description (the header part of --help)
Alice: That makes sense. Reading further in binary_diagnostics,
I see that you enter a double loop over all the bodies in a snapshot, and
for each possible pair you check to see whether that pair of bodies is
currently forming a binary.
3.4. The World Level
3.5. Binary Diagnostics in Action
|gravity> kali world4.rb ---help
This program evolves an N-body code with a fourth-order Hermite Scheme,
using individual time steps. Note that the program can be forced to let
all particles share the same (variable) time step with the option -a.
This is a test version, for the ACS data format
(c) 2005, Piet Hut, Jun Makino; see ACS at www.artcompsi.org
example:
kali mkplummer.rb -n 4 -s 1 | kali world4.rb -t 1
So you suggest I literally do that? Let me try:
|gravity> kali mkplummer.rb -n 4 -s 1 | kali world4.rb -t 1
==> Plummer's Model Builder <==
Number of particles : N = 4
pseudorandom number seed given : 1
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
actual seed used : 1
==> Individual Time Step, Individual Integration Scheme Code <==
Choice of integration method : integration_method = hermite
Determines the time step size : dt_param = 0.01
Initial timescale factor : init_timescale_factor = 0.01
Duration of an era : dt_era = 0.0078125
Maximum time step (units dt_era): dt_max_param = 1.0
Diagnostics output interval : dt_dia = 1.0
Snapshot output interval : dt_out = 1.0
Prune Factor : prune_factor = 0
Duration of the integration : t = 1.0
Max cputime diagnost. interval : cpu_time_max = 60
Maximum semi-major axis : max_semi_major_axis = 1.0e+30
Binary Diagnostics Precision : binary_diag_precision = 4
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
t = 0 (after 0, 0, 0 steps <,=,> t)
E_kin = 0.25 , E_pot = -0.5 , E_tot = -0.25
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
[0, 1] : a = 2.1938e+00 ; e = 6.9252e-01 ; T = 2.8872e+01
[1, 2] : a = 1.8007e-01 ; e = 8.8222e-01 ; T = 6.7900e-01
t = 1 (after 4329, 0, 6 steps <,=,> t)
E_kin = 0.313 , E_pot = -0.563 , E_tot = -0.25
E_tot - E_init = 1.64e-10
(E_tot - E_init) / E_init = -6.58e-10
[0, 1] : a = 4.9021e-01 ; e = 8.4660e-01 ; T = 3.0498e+00
[1, 2] : a = 1.8175e-01 ; e = 9.4611e-01 ; T = 6.8852e-01
ACS
NBody
Array body
Body body[0]
Vector acc
4.3680007628230150e-01 -7.7920066607005689e-01 -3.4447512499978329e-02
Array acsmixins
Module acsmixins[0]
Integrator_hermite
Fixnum body_id
0
Float dt_param
1.0000000000000000e-02
Vector jerk
3.2148293860481963e-01 1.5455084837998969e+00 5.0309934483466201e-01
Float mass
2.5000000000000000e-01
Float maxstep
5.3298829935937153e-03
Float minstep
2.8993571645200446e-05
Float next_time
1.0026061296123183e+00
Fixnum nsteps
332
Vector pos
7.9772604070178846e-03 8.2919239954665480e-01 8.6949862920921966e-02
Float time
1.0000000000000000e+00
Vector vel
-6.0338461103000307e-01 -2.5365567416813917e-01 -4.2283983072465980e-01
Body body[1]
Vector acc
2.9407213696345624e+00 4.3737103517008107e+00 2.8696484413452512e+00
Array acsmixins
Module acsmixins[0]
Integrator_hermite
Fixnum body_id
1
Float dt_param
1.0000000000000000e-02
Vector jerk
-3.0679123445456916e+01 -6.0941785672989397e+01 -4.1544144235617914e+01
Float mass
2.5000000000000000e-01
Float maxstep
2.8967962731903940e-03
Float minstep
1.0126966959234096e-05
Float next_time
1.0007045202601113e+00
Fixnum nsteps
1933
Vector pos
3.4274367211420625e-01 1.1210653405826151e-01 6.9410494803967479e-03
Float time
1.0000000000000000e+00
Vector vel
-1.7471717282768337e-01 -4.6103585065601543e-01 -3.2046114392320907e-01
Body body[2]
Vector acc
-3.4927708485553790e+00 -3.7533254304484691e+00 -2.8624660563443318e+00
Array acsmixins
Module acsmixins[0]
Integrator_hermite
Fixnum body_id
2
Float dt_param
1.0000000000000000e-02
Vector jerk
3.0274773693388109e+01 5.9364365363757656e+01 4.1104361307013662e+01
Float mass
2.5000000000000000e-01
Float maxstep
2.8967962777788347e-03
Float minstep
1.0126966976886642e-05
Float next_time
1.0007045842393165e+00
Fixnum nsteps
1933
Vector pos
4.5401351630391895e-01 2.5523386444086688e-01 1.0661490776678197e-01
Float time
1.0000000000000000e+00
Vector vel
9.5626266521217429e-01 2.6335235690235648e-01 2.0752875999010723e-01
Body body[3]
Vector acc
1.1435586922134454e-01 1.5721237097257557e-01 2.7242540252499236e-02
Array acsmixins
Module acsmixins[0]
Integrator_hermite
Fixnum body_id
3
Float dt_param
1.0000000000000000e-02
Vector jerk
8.8699613819200801e-02 3.4954588596844444e-02 -6.0072687819262158e-02
Float mass
2.5000000000000000e-01
Float maxstep
7.8125000000000278e-03
Float minstep
1.6386823913682258e-04
Float next_time
1.0002615373733836e+00
Fixnum nsteps
135
Vector pos
-8.0473444786322912e-01 -1.1965327941527619e+00 -2.0050581825457850e-01
Float time
1.0000000000000000e+00
Vector vel
-1.7816088524364576e-01 4.5133917639638632e-01 5.3577221678447662e-01
String story 2
t = 0 (after 0, 0, 0 steps <,=,> t)
E_kin = 0.25 , E_pot = -0.5 , E_tot = -0.25
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
[0, 1] : a = 2.1938e+00 ; e = 6.9252e-01 ; T = 2.8872e+01
[1, 2] : a = 1.8007e-01 ; e = 8.8222e-01 ; T = 6.7900e-01
t = 1 (after 4329, 0, 6 steps <,=,> t)
E_kin = 0.313 , E_pot = -0.563 , E_tot = -0.25
E_tot - E_init = 1.64e-10
(E_tot - E_init) / E_init = -6.58e-10
[0, 1] : a = 4.9021e-01 ; e = 8.4660e-01 ; T = 3.0498e+00
[1, 2] : a = 1.8175e-01 ; e = 9.4611e-01 ; T = 6.8852e-01
Float time
1.0000000000000000e+00
SCA
3.6. Taming the Flow of Output
|gravity> kali mkplummer.rb -n 4 -s 1 > tmp.in
==> Plummer's Model Builder <==
Number of particles : N = 4
pseudorandom number seed given : 1
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
actual seed used : 1
|gravity> kali world4.rb -t 1 -o 1000 -x 0.5 --binary_diag_precision 2 < tmp.in
==> Individual Time Step, Individual Integration Scheme Code <==
Choice of integration method : integration_method = hermite
Determines the time step size : dt_param = 0.01
Initial timescale factor : init_timescale_factor = 0.01
Duration of an era : dt_era = 0.0078125
Maximum time step (units dt_era): dt_max_param = 1.0
Diagnostics output interval : dt_dia = 1.0
Snapshot output interval : dt_out = 1000.0
Prune Factor : prune_factor = 0
Duration of the integration : t = 1.0
Max cputime diagnost. interval : cpu_time_max = 60
Maximum semi-major axis : max_semi_major_axis = 0.5
Binary Diagnostics Precision : binary_diag_precision = 2
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
t = 0 (after 0, 0, 0 steps <,=,> t)
E_kin = 0.25 , E_pot = -0.5 , E_tot = -0.25
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
[1, 2] : a = 1.80e-01 ; e = 8.82e-01 ; T = 6.79e-01
t = 1 (after 4329, 0, 6 steps <,=,> t)
E_kin = 0.313 , E_pot = -0.563 , E_tot = -0.25
E_tot - E_init = 1.64e-10
(E_tot - E_init) / E_init = -6.58e-10
[0, 1] : a = 4.90e-01 ; e = 8.47e-01 ; T = 3.05e+00
[1, 2] : a = 1.82e-01 ; e = 9.46e-01 ; T = 6.89e-01
Bob: Just what you ordered!