5. Recycling Force Evaluations
%\subsubsubsection{General Form}
{\bf 4.2.1.1. General Form}
5.1. One Force Evaluation per Step
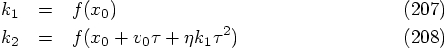
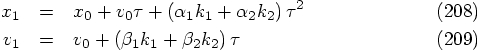
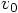 in
in 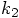 should be
should be 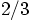 ,
and not
,
and not 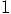 as we insist upon above. [EXPAND THIS]
as we insist upon above. [EXPAND THIS]
This means that we only have to expand up to powers in 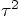 .
.
with

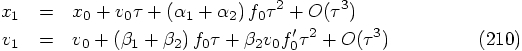
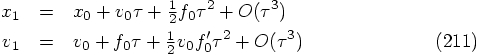



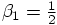 . Two parameter freedom,
with
. Two parameter freedom,
with 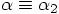 :
:
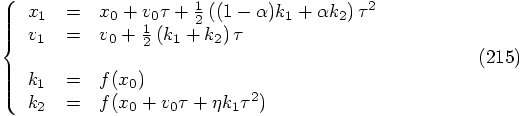
{\bf 4.2.1.2. Second Order Recycle Conditions}
Now insist that 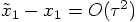 :
:
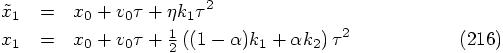
For 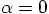 and
and 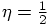 , simplest choice: leapfrog.
, simplest choice: leapfrog.
[check for which values time symmetry;
presumably only for 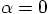 and
and 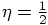 ]
]
%\subsubsubsection{General Form}
{\bf 4.2.2.1. General Form}
{\bf 4.2.2.2. Third Order Recycle Conditions}
Now insist that
From the last two:
Another example: for
{\bf 4.2.2.3. Exact Recycling}
So far, only pseudo-FSAL, or better: pseudo Runge Kutta!
Can we make it really FSAL Runge Kutta, to all orders?
%\subsubsubsection{A Search for a Fourth Order Scheme}
{\bf 4.2.2.4. A Search for a Fourth Order Scheme}
Given that we have three free parameters left in our construction of a
recycling scheme that is third order correct, it is tempting to search
for a fourth-order scheme, based on only two new force calculations
per time step.
Repeating the previous analysis to one order higher in
We thus have:
By the way, as a fourth-order scheme, it is listed in Abramowitz and
Stegun's welknown Handbook of Mathematical Functions as eq. 25.5.22,
but with a typo: the error in the position is listed as being
5.2. Two Force Evaluations per Step
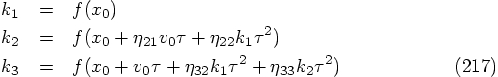
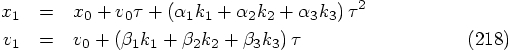
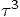 .
.
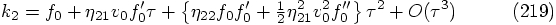
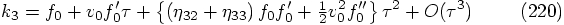
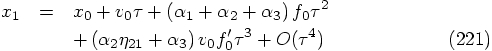
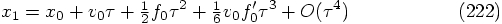


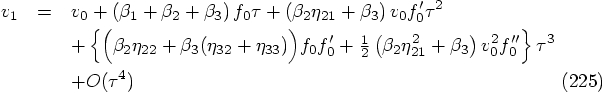
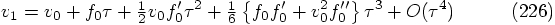



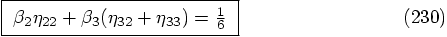
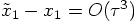 :
:
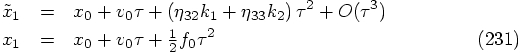



 or
or  .
In the first case,
.
In the first case, 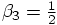 and
and 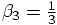 from the
next to last equation and the one above that. Contradiction. Hence:
from the
next to last equation and the one above that. Contradiction. Hence:

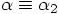 and
and 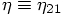 , and use
, and use
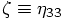 as the third parameter.
Then
as the third parameter.
Then
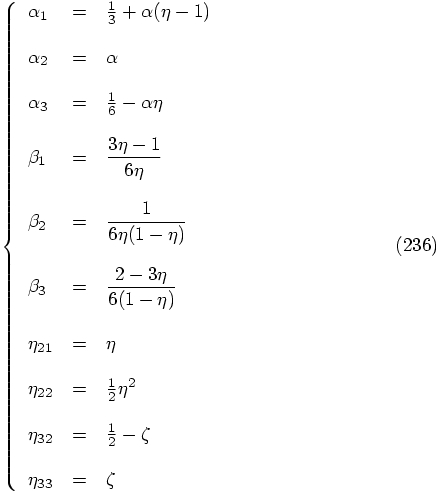
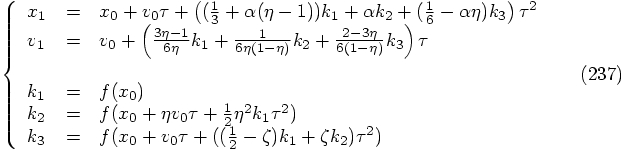
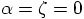 ,
, 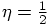 :
:
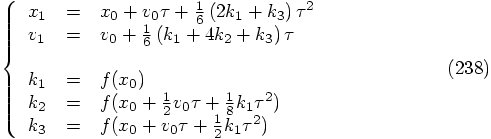
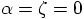 ,
, 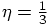 :
:
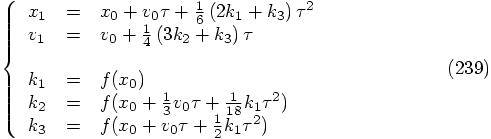







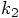 and
and 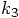 terms
in the expression for
terms
in the expression for 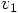 in Eq. (237) blow up.
in Eq. (237) blow up.
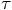 , we get
, we get
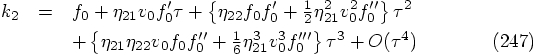
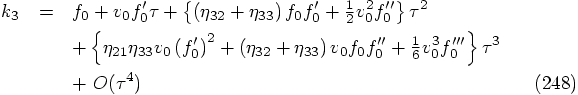
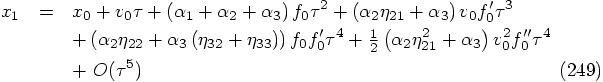
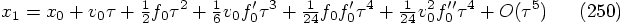
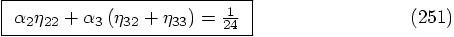

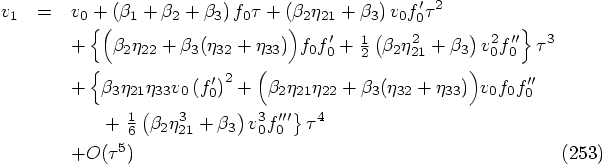
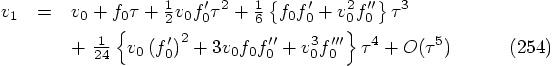

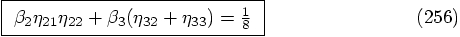

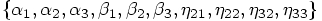 . A priori
we would expect to find no solutions in such an overdetermined system.
However, let's see how far we get when we try. Let us list the
conditions here together:
. A priori
we would expect to find no solutions in such an overdetermined system.
However, let's see how far we get when we try. Let us list the
conditions here together:
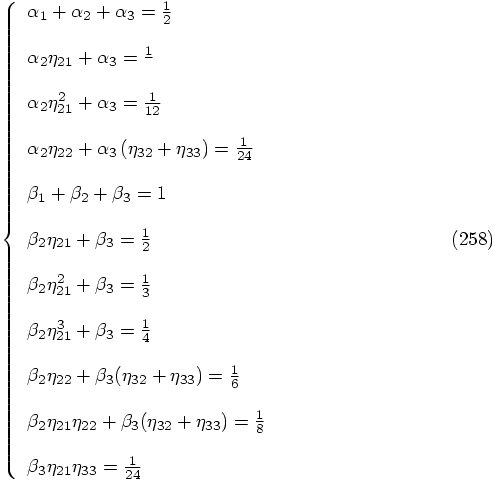


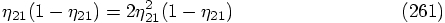
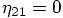 ,
, 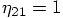 , and
, and
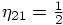 . The first two solutions can be discarded, because
they would imply that the left-hand side of the 6th, 7th, and 8th
equations above would all have the same value, contradicting the fact
that their right-hand sides have different values. We thus find
. The first two solutions can be discarded, because
they would imply that the left-hand side of the 6th, 7th, and 8th
equations above would all have the same value, contradicting the fact
that their right-hand sides have different values. We thus find















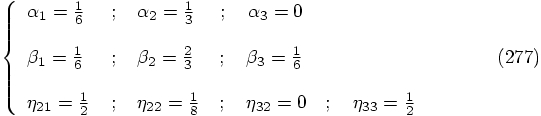
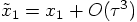 , which was
, which was

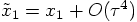 ? If that were true,
our fourth-order scheme would allow us to recycle the last force
calculation, and we would really have obtained a fourth-order scheme
with an effective costs of only two new force calculations per step.
This does sound too good to be true, but let's just check.
? If that were true,
our fourth-order scheme would allow us to recycle the last force
calculation, and we would really have obtained a fourth-order scheme
with an effective costs of only two new force calculations per step.
This does sound too good to be true, but let's just check.
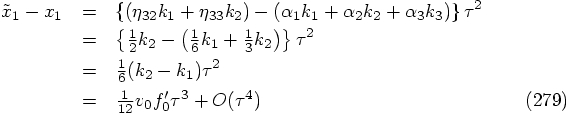
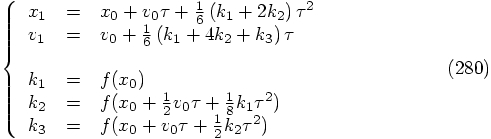
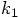 term which the
former lacks, and since the difference
term which the
former lacks, and since the difference 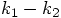 is of first order
in
is of first order
in 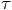 , there is a real third-order difference between the two
positions, hence between the forces computed in these two positions.
The upshot is that this will introduce a fourth-order error in the
velocity in the next step, when we recycle the last force calculation.
Our scheme is thus only third-order accurate when we recycle, even
though it is fourth-order accurate if we decide to compute all three
new forces anew at each step.
, there is a real third-order difference between the two
positions, hence between the forces computed in these two positions.
The upshot is that this will introduce a fourth-order error in the
velocity in the next step, when we recycle the last force calculation.
Our scheme is thus only third-order accurate when we recycle, even
though it is fourth-order accurate if we decide to compute all three
new forces anew at each step.
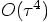 , while it really should be
, while it really should be 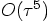 ; in addition no
error is listed for the velocity. As we have seen, for the velocity,
too, the error is
; in addition no
error is listed for the velocity. As we have seen, for the velocity,
too, the error is 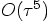 .
.