0. Preface
In this volume, we present a pedagogic overview of the freedom one has
in choosing the coefficients in explicit Runge-Kutta integration
schemes. We limit ourselves to the simple cases in which there are at
most two new evaluations of the right-hand side of the differential
equation per time step. We start with first-order differential
equations, to explain the general procedures, but then we limit
ourselves to the type of second-order differential equation that
occurs in classical mechanics, where the forces are dependent only on
positions, and independent of the velocities. In that case we derive
some of the classical 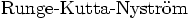 schemes, and
generalize this to include a first evaluation that does not take place
at the beginning of a time step. We show how such a generalized
approach naturally leads us to the
schemes, and
generalize this to include a first evaluation that does not take place
at the beginning of a time step. We show how such a generalized
approach naturally leads us to the
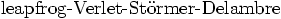 scheme, as a particular
form of a generalized explicit Runge-Kutta scheme.
scheme, as a particular
form of a generalized explicit Runge-Kutta scheme.