4. Input and Output
Alice: So where are we? We have successfully defined a class Body,
and have learned to give it initial values and to print those out.
Shall we code up an integrator?
Bob: Before we do that, I would prefer to get the right I/O tools in
place first. On the level of input, we can type in the values by hand
when we create a particle, but we have not yet learned how to read
particle data from a file. And on the level of output, we really should
figure out how to print particle data in 64-bit floating point
accuracy, often called "double precision" for historical reasons.
Alice: Why do you want to be so accurate?
Bob: There will be many cases where we integrate the orbit for an
N-body system for a while, save the data, and then later continue the
integration. If we don't save the data to the same level of accuracy
as what is used in the internal calculations, we will lose precision.
Alice: Good point. Let us get our basic tools ready then. Isn't it
interesting that learning the I/O always seems to be one of the trickiest
parts of learning a new language?
Bob: That must be because all the internal computations take place in
a separate universe, defined fully by the language specification. It
is only at I/O times that a language is forced to interface with the
world. And this necessarily brings in much more baggage.
Most languages specify a simple but rather rigid way to do I/O, as a
default. But sooner or later you need more control, for particular
purposes, and that requires more complicated I/O routines, with a more
complicated syntax.
In other words, doing your own thing is a lot easier than interfacing
with the world.
Alice: I'm glad to see you stressing interface issues! Everything
that you said about I/O applies to the way I think the various modules
in an N-body code should communicate. For each module, there is a
well controlled internal environment, that has to interface with a
wild world out there, over which the module has no control, and from
which the module has to protect itself, so that it does not get
tripped by confusing signals
Bob: You always have an excuse to talk about principles, just when
we're about to do some real work. Let's get our double precision first.
And because we are writing a toy model, I suggest we do our I/O in ASCII,
not in binary form.
Alice: Absolutely. I am always happier when I can look into a file,
and see the data there directly, without everything being encoded in
some weird way. Such encryptions are often machine dependent anyway, and
ASCII characters are platform independent.
But in that case, we'd better print everything out with enough digits.
Let's look at the web. The IEEE 64-bit floating point number definition
specifies 1 bit for the sign, 11 bits for the exponent, and the remaining
52 bits for the mantissa.
Bob: No, there are effectively 53 digits. By definition of floating point
notation, the most significant digit of the mantissa is always 1, and
cleverly the IEEE people have defined their standard so that that 1 is
being left out. Effectively we are using 65-bit precision in double
precision calculations on our computers.
Alice: I had no idea! But
Bob: I should be able to figure out how to do this. I like this kind of
tinkering.
Alice: I'm glad you do! I'll get a cup of tea in the meantime.
Bob: Yes, it works! But let me first show you what it all means.
The printf statement in the second line comes straight from C. It
specifies that the mass will be printed in a field that is 24 characters
wide, with 16 decimal places of precision.
The third line shows a nice Ruby feature: each array knows how long it
is, so instead of stepping through the array with a do loop or for loop,
you can simply ask an array to do something for each of its elements.
pos.each invokes the method each that is built in already
within the class Array. It is called an iterator.
Alice: I presume it corresponds to the use of iterators in the C++
standard template library. But it looks quite a bit simpler. Instead
of first asking the array for its begin and end, and then looping over
the elements in between, here the one word each does the whole job.
Bob: Welcome to Ruby! What the iterator does to each element is
specified in the region between the parentheses, immediately following
each. First comes a variable name x between bars, that stands for
the name of each element of the array, while the array is traversed.
In this case, each element is printed in the same format as we printed
the mass in the previous line.
Alice: The simple_read method puzzles me. What is this gets
in the first line?
Bob: It is short for `get string': it reads in one line of input, and
returns as its value the string of characters that it has read in.
Alice: Ah, and to_f converts the string, as a collection of
characters, to a floating point value, just as atof would do in C.
Bob: Exactly. And the important thing to notice here is that gets
returns a string, which in Ruby is an instance of the class String.
And this to_f is a method associated with that class -- it plays the
role that a member function plays in C++, as we saw before. You can
ask an object to invoke one of its methods by putting a dot in between
the object and a method. And by implication this is what happens to
the object returned by gets.
Alice: The principle of least surprise all right.
Bob: As you can see in simple_print, I have chosen a data
format in which a single particle prints its mass, position, and
velocity on three consecutive lines. To be compatible,
simple_read should perform a separate gets for
@mass, for @mpos, and for @vel.
The trickiest thing to get right was to read the three components
from a vector. Here I have used split which is a string method that
splits the string into smaller chunks, and then returns an array which
contains each chunk as an element. If you want, you can specify the
way a string is being split into such subarrays, by giving a parameter
to split, but the default delimiter is white space.
Now map is an array method that takes each element of the array
in turn, and executes a block of code for that element. The syntax is
the same as what we saw for each above. The block is delimited by
curly braces, and the free variable that loops over the array elements
is specified by the vertical bars. The rest of the block contains the
commands that are executed for each element. In our case each component
of the position is converted into a floating point number, and the same
happens for the velocity on the next line.
By the way, map is actually an alias for collect, and you can use
both words interchangeably for the same method. Because this method
effectively `maps' an action onto each element and then `collects'
the results into a new array, each word describes part of the process.
I prefer map both because it is shorter and because it describes the
step where the actual work is done. In Ruby, there are many examples
of such aliases. To find the length of an array a, for example, you
can equally well use a.length as a.size. Sometimes
you even have freedom in spelling: a.indexes and
a.indices do the exact same thing. I consider all this
freedom another friendly aspect of Ruby.
Alice: The only drawback is that when you look at someone else's
program, you might be surprised to see someone using unfamiliar
aliases. However, I presume that you get used to that pretty quickly.
What I am curious about is that you haven't specified anywhere that we
live in three dimensions. I find that pretty remarkable: in Fortran
or C or C++, you could not get away with that. This must mean that
the code will work equally well for a two-dimensional simulation,
where a body has position and velocity vectors with only two
components, as for a three-dimensional simulation.
Bob: Right you are, and that indeed gives you a wonderful flexibility.
In C you would first define #define NDIM 3, and then specify
something like for (k = 0, k < NDIM, k++) followed by the
block of code you would loop over, containing expressions like
pos[k] for the kth element of the position vector. What a
breeze this is, by comparison!
Alice: Remarkable. Once you gain familiarity with those notions such
as gets and split and map, it must become second nature to
string a few together. The result is a notation that is compact, yet
still informative. Can you show me that all this really works?
Bob: Here is what I wrote in our test file
test.rb, immediately following the Body class definition:
As you can see, I create a new blank Body, and I immediately perform
an input. This means that we have to put in the values by hand, on
three consecutive lines, one for each internal variable. The script
then performs an output, printing out the particle state. Here is an
example.
Bob: My pleasure:
Actually, this would be an appropriate way to view this script: when
we finish our integrator, it will transform initial conditions to
final conditions after a certain time t. In other words, the
integrator will act as a propagator, mapping initial conditions onto
final conditions.
Bob: I'm glad you haven't forgotten the goal of these exercises, to
move particles around. The term `propagator' comes from elementary
particle physics, I presume? Well, I guess that our point particles
are about as elementary as they come, so it is not altogether
inappropriate.
Alice: Before we get going with our particle pushing, I can't help
wondering whether you can't further simplify your reading and writing
routines. I bet these were not what you first wrote down; you must
have compactified things already.
Bob: You're right. My first attempt at the read method was a lot
longer. Here, I still have it:
Bob: In Ruby there is a general convention that a command followed
by an exclamation mark in its name does the same thing as the command
without that exclamation mark, but it does it to the object it is
associated with. Here map!operates on the array a that
is calling the method. Previously, I used map which
returns a new array that contains the values resulting from the
operations. Be careful here: the bang sign "!" is not an operator
in itself, it is only an allowed character for the last part of the
name of a command. It is up to the code writer to choose sensible
names such that do_something and do_something! do the same
thing, the first one producing a new array, and the second one
changing the elements of the array on which it was called.
Alice: So you managed to reduce the number of lines of your method
by a factor of three, presumably also in your write method. Currently
you have three lines left in each method. Can I challenge you to
reduce it even further?
Bob: By another factor of three? But that would only leave one line
for each method. Are you serious?
Alice: Well, not really. But I'm still thirsty. Let me get us
some more tea.
Bob: Here is the keyboard. Try it.
Bob: I must admit, I surprised myself. But then again, you asked,
and I like to take up a challenge. Would you like to know how/why
it works?
Alice: Hmmm. Perhaps not in detail yet. Since I was going to look
at the manual tonight, this will give me my own challenge: to figure
this one out. 4.1. Double Precision Input/Output
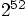is less than
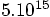, so 16 digits should be enough.
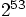is about
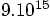, so 16 digits is still enough. I was lucky there.
4.2. A Simple Version
. . .
Here's a cup for you too. Ah, that looks impressively short. Is that
really enough to do the job?
4.3. Trying It Out
b = Body.new()
b.simple_read
b.simple_print
|gravity> ruby test.rb
3
0.1 0.2 0.3
4 5 6
3.0000000000000000e+00
1.0000000000000001e-01 2.0000000000000001e-01 2.9999999999999999e-01
4.0000000000000000e+00 5.0000000000000000e+00 6.0000000000000000e+00
Alice: Very good. And since we can now read and write, how about
testing your script by reading what you just wrote out? We can pipe
the output into another invocation of test.rb.
|gravity> ruby test.rb | ruby test.rb
3
0.1 0.2 0.3
4 5 6
3.0000000000000000e+00
1.0000000000000001e-01 2.0000000000000001e-01 2.9999999999999999e-01
4.0000000000000000e+00 5.0000000000000000e+00 6.0000000000000000e+00
Alice: Congratulations! This is what a mathematician would call a
fixed point, if we would view the operation ruby test.rb
as a mapping.
def read
s = gets
@mass = s.to_f
s = gets
a = s.split
a.map! { |x| x.to_f }
@pos = a
s = gets
a = s.split
a.map! { |x| x.to_f }
@vel = a
end
Alice: Quite a reduction. But why the exclamation marks after map ?
4.4. A Surprise
. . .
Here's another cup. WHAT? Are you serious? Does that work???
def simple_print
[[@mass],@pos,@vel].each{|x| x.each{|y| printf("%24.16e",y)}; print "\n"}
end
def simple_read
(@mass,),@pos,@vel = (1..3).map{|i| i = gets.split.map{|x| x.to_f}}
end
|gravity> ruby test.rb
8
0.2 2 20
10 1 0.5
8.0000000000000000e+00
2.0000000000000001e-01 2.0000000000000000e+00 2.0000000000000000e+01
1.0000000000000000e+01 1.0000000000000000e+00 5.0000000000000000e-01
Alice: I'm shocked. How can you do input in one line and output
in one line for a whole particle, with a heterogeneous data set? Even
writing this question down would take more than one line of text!