6. Orbit Integration
Bob: Time to test our Forward Euler code!
Alice: I see there is a call to simple_read, so I presume we have
to provide an input file, that will contain the initial conditions,
from which we can then start to integrate the equations of motion.
Bob: Let's call it euler.in; how about this one?
Bob: That may not be immediately obvious for a student. When I heard
this for the first time, I thought about two particles passing each
other at right angles at a distance, like the two arms of a cross but
then offset in the third dimension.
Alice: You are right. The best way to convince a student is probably
to let her or him do the exercise of translating the motion to the
center of mass system of the two particles. In that system, the
motion of the one particle is the same but opposite as the motion of
the other particle, apart from a scaling factor involving the ratios
of the two masses. The position vector of one particle as defined
from the center of mass, together with the velocity vector of that
particle, spans a unique plane. The fact that the other particle
moves in the (scaled) opposite way then implies that the other
particle moves in the same plane as well.
Bob: Yes, even if you know the answer, it always requires some thinking
to reconstruct the reason for the answer. So because a two-body
problem is inherently two-dimensional, we might as well start with
specifying only two components for the position and velocity of the
relative motion of the two particles, which made me choose the above
numbers. Total mass of unity, initial position on the x-axis, also
unity, and initial velocity perpendicular to that, and one half, for a
change.
Bob: Time to test our Forward Euler code:
Bob: And look, the velocity has increased. It started off with
vector length unity, and now it is about 1.3 length. Since we started
with a velocity direction perpendicular to the line connecting both
particles, we were either at pericenter or apocenter.
Alice: You'll have to explain that to the students.
Bob: Pericenter is the point in a Kepler orbit where the distance
between two particles is smaller than anywhere else in that orbit.
The apocenter is reached when the two particles are furthest away
from each other. From the Greek peri or near, and apo or away.
Now if you are closest, you move fastest, since the gravitational
force is larger at smaller distances. Similarly, when you are at
apocenter, you move slowest. Moving away from pericenter, you slow
down, while moving away from apocenter you speed up. Ergo: we
obviously started the particles at the maximum distance, given their
energy and angular momentum, specified at the start.
But all this will makes much more sense to the students when we show
them the orbit with some real graphics. We'll come to that soon. For
now, let's make sure that the integrator does what it is supposed to do.
Let me make the step size ten times smaller, to see whether we get
roughly the same answer. I will make the number of time steps ten
times larger, to make sure the integration time stays the same:
And then we run it:
Bob: That's about all that I would have expected from such a simple
integrator.
Alice: How do we expect things to scale
when we will make the time step even smaller? We are dealing with a
first order integrator. How did that go?
Bob: A first order integrator is first-order accurate. which means
that the errors per time step are quadratic in the size of the time
step. Making the time step ten times as small will give you errors
that are each one hundred times as small. However, you have ten times
more steps, so if the errors are systematic, as they often are, the
total error is ten times larger than a single error per time step.
In other words, making the time step ten times smaller will make the
total error will go down also by a factor of ten.
Or so I think. Let me put in the values
and run it:
Bob: Let me push my luck with another factor of ten
and see whether the trend continues:
Alice: Before we declare victory, I'd like to see us integrating at
least a full orbit. How about increasing the time from 1 to 10 time
units? That should be more than enough.
Bob: I would think so. With a total mass of one and an initial
distance of one, in a system of units where the gravitational constant
Alice: Something like that, but it could be a bit smaller. We started
at apocenter, which means that the relative motion is speeding up. In
fact, we saw before that the velocity had increased. Anyway, pretty
soon we'll have to install some form of graphics, since I'd sure like
to see the orbit, rather than staring at numbers. But one thing at a
time; we'll get to that soon.
Bob: Here is an integration for ten time units, starting with our
original time step of 0.01:
For one time unit we got a position error of order one percent, for
a time step of 0.01. For ten time units we may expect ten or twenty
percent, I guess. But in order to get an estimate of our errors we
have to do at least two runs, to compare. So we'll do this run first,
and then we'll do a run with much smaller time steps. Here is the
first run.
Bob: With expected errors of a few tens of percent it is easy to
get into a nonlinear regime. And come to think of it, our relative
particle motion was headed for pericenter, where the distance between
the particles gets smaller, the inverse square law force increases even
faster, and the curvature of the orbit becomes larger as well. And
since we have constant time steps, the errors per time step can be
expected to be quite a bit larger.
Alice: How much larger?
Bob: I'm sure we can derive that easily, but let's be lazy and ask
the computer. Later we can be more systematic about all this, when we
start implementing higher order integrators. So let's go down with
powers of ten again in time steps:
I hope the relative motion behaves better now.
Alice: Better already. Still too far, at a relative distance of more
than two, but not as outrageous as before. Another step of ten down?
Bob: My pleasure:
Bob: But unless we really converge, I for one won't believe it quite yet.
Alice: If we are really converging, with a first-order integrator,
we should see the errors shrinking by a factor of ten.
Bob: Let's check. But the computer sure took its time to give us
that last result. Something tells me that Ruby is not very fast at
numerical calculations
This may take a while, ten times longer than the previous run!
Alice: You're right. With a C or Fortran code, doing a million time
steps should take much less than a second. There must be a huge
efficiency factor involved.
Bob: Perhaps not too surprising, given that Ruby is an interpreted
language. And besides, the fact that it allows such short and
powerful expression must mean that a lot is going on behind the
scenes. One of the books I looked at mentioned that almost everything
in Ruby is done not just with one level of redirection, as you might
expect, but with two levels of redirection!
Alice: That makes you wonder about the wisdom of choosing Ruby for a
computationally intensive project.
Bob: That's what I thought all along, but . . .
Alice: . . . you mean, it's no problem for a student project, as a toy
model?
Bob: No, it is a problem, even for a student project. Which
student would want to have to drink a cup of coffee before he or she
can integrate a few orbits in a Kepler problem? Ruby must be at least
two orders of magnitude slower than C or Fortran.
Alice: Does this mean that we have to abandon our pretty new language?
Bob: Not at all! What I was about to say is: I was worried about speed,
at first, but then I read on the net that it is quite easy to speed Ruby
programs up, simply by replacing the most compute-intensive part of the
code by a small C program, which then gets called from Ruby. The way it
was described was rather simple, and I expect that we can regain most of
the speed we now have lost.
Alice: I sure hope so. I'm quickly growing fond of Ruby. As soon as
we get a chance, let's test it for ourselves.
Bob: Will do! Hey, we finally got an answer:
Bob: But I was wrong in thinking that the error would be only a few
percent. It is still about ten percent in the x position, and even
more in the y component of the velocity. I want to get to the
bottom of this. Let us send Ruby out for a long errand, with one
hundred million time steps:
We may as well get a bit to eat, since we can't wait for this to finish.
Alice: Good idea.
Alice: And look, Ruby has done it's job. Now the error is down to
about one percent in any of the position or velocity coordinates.
Bob: Good! Now I believe that we have done things correctly. But boy,
that took a long time to converge. Two morals of the story: to do anything
at all in orbit calculations, you must use a higher-order integrator, and
you'd better speed up its inner loop if you are using an interpreted language. 6.1. Two Dimensions
1
1 0
0 0.5
Alice: A nice example of our dimensional freedom: a
two-body problem is intrinsically two-dimensional. It was not just
laziness that I showed the equations in component form only for two
dimensions. Even in three dimensions, a 2-body problem can always
be reduced to a two-dimensional problem. The point is that you can
always find a plane in which the relative motion takes place.
6.2. Forward
|gravity> ruby test.rb < euler.in
mass = 1.0
pos = 0.443229564341409, 0.384215558686636
vel = -1.29436531289392, 0.0258120006669036
Alice: That looks reasonable. We started with a relative velocity
of 0.5, so in one time unit of integration, you would expect the
position vector to have changed by something like half a length unit.
We started with position {1.00, 0.00} and we now have {0.44, 0.38}.
So we have crossed a distance vector of {-0.56, 0.38}, which has a
length of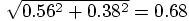 
, not far from one
half.
dt = 0.001 # time step size
ns = 1000 # number of time steps
|gravity> ruby test.rb < euler.in
mass = 1.0
pos = 0.433021780531577, 0.37860453335417
vel = -1.31479264498764, 0.00718433856141339
Alice: Not bad, for such a simple integrator. The differences with
the previous run are typically only one unit in the second decimal
place, in each vector component.
6.3. Error Scaling
dt = 0.0001 # time step size
ns = 10000 # number of time steps
|gravity> ruby test.rb < euler.in
mass = 1.0
pos = 0.431974652285879, 0.378023068595097
vel = -1.31693301875844, 0.00522927166213894
Alice: How nice. The differences between the last two runs are
now mostly one unit in the third decimal place. Just as you predicted!
dt = 0.00001 # time step size
ns = 100000 # number of time steps
|gravity> ruby test.rb < euler.in
mass = 1.0
pos = 0.431869664380511, 0.377964708368075
vel = -1.31714808792365, 0.00503278405037421
It does. Differences of one unit in the fourth decimal place. And
most of the differences in comparing the last two runs must come from
the much less accurate run before the last one. So the last one can
be expected to be accurate to about one unit in the fifth decimal
place. So it would seem safe to say that the first component of the
relative position will be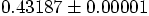 
. I think
we have shown that we can solve the 2-body problem with Ruby!
6.4. A Full Orbit
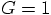as well, the orbital period should be of order unity.
But there must be a factor 
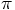somewhere in there as well.
My guess would be that the period would be at least five, in our units,
given that the relative motion started on the right hand side of the
x axis moving upward, and after one time unit we are still in the
first quadrant, with positive y and x values.
dt = 0.01 # time step size
ns = 1000 # number of time steps
|gravity> ruby test.rb < euler.in
mass = 1.0
pos = 7.6937453936572, -6.27772005661599
vel = 0.812206830641815, -0.574200201239989
Alice: Hmmm. Whatever the second run will be, the error must be
quite a bit more than twenty percent, I'd say. After you explained
that the initial position was at apocenter, we should never encounter
a situation where the particles are at a relative distance of more
than unity. And here we have a distance of more than seven, in fact
almost a distance of ten units!
dt = 0.001 # time step size
ns = 10000 # number of time steps
|gravity> ruby test.rb < euler.in
mass = 1.0
pos = 2.01435512882368, 0.162565336385657
vel = -0.152875528688122, 0.258696442895482
6.5. Taking Time
dt = 0.0001 # time step size
ns = 100000 # number of time steps
|gravity> ruby test.rb < euler.in
mass = 1.0
pos = 0.292716737826681, 0.38290774857968
vel = -1.56551896976999, -0.313957063867402
Alice: Ah. Much better. This begins to be believable.
dt = 0.00001 # time step size
ns = 1000000 # number of time steps
|gravity> ruby test.rb < euler.in
mass = 1.0
pos = 0.519970642634004, -0.376817992041834
vel = 1.17126787143698, 0.114700879739653
Ah, perhaps we are getting there. Now we have a difference between runs
that is closer to what I had hoped for, a few tenths of percent.
dt = 0.000001 # time step size
ns = 10000000 # number of time steps
6.6. Convergence
|gravity> time ruby test.rb < euler.in
mass = 1.0
pos = 0.592168165567474, -0.362592197667279
vel = 1.04418312945112, 0.205156629088709
Alice: And you were right: it is converging.
dt = 0.0000001 # time step size
ns = 100000000 # number of time steps
. . . .
|gravity> time ruby test.rb < euler.in
mass = 1.0
pos = 0.598877592948656, -0.360833442654858
vel = 1.03213853108295, 0.213031665991379
Bob: That was not bad, to stretch our legs and get some good food.
A nice side effect of a slow integration.