11. Testing Forward Euler
Bob: Time to run the driver for our new integrator,
which will give us the energy conservation diagnostics
we have been talking about for so long now! Let us start
with the same variables we used for our very first forward
Euler run:
We concluded that the position was probably right to within
a percent or so, from comparing it with a more accurate
integration. I'm curious whether the energy check gives us
a similar answer.
Bob: That was just pure luck, my argument was only an order of
magnitude estimate.
Alice: As we argued, a first-order method like the forward Euler
should converge linearly: making the step size ten times smaller
should decrease the error size also by roughly a factor of ten.
Shall we try?
Bob: So we expect an error of
making the time step smaller by a jump of a factor of a hundred.
Alice: Let's follow your earlier suggestion to do a longer integration,
for ten time units. And let's use your flexible output options. I would
like to see four energy diagnostics, but at most one final position and
velocity output, so that we don't get too distracted.
Bob: That means:
I have given dt_out a value larger than the total run time
dt_end, so we won't get the regular particle output, only
the diagnostics.
Bob: Ah yes, this was the run where the system exploded, with the
relative distance increasing to a value of about ten.
Alice: And look, the velocity vector is almost parallel to the position
vector, and pointing in the same direction. Clearly, the two bodies are
escaping from each other.
Bob: And that explains why the energy error is frozen: there is no longer
much interaction going on between the particles. The numerical explosion
must have happened at pericenter, as we deduced earlier. Let's have a
closer look at what happens in the first part:
A four times shorter run, with five times more frequent diagnostics.
Bob: Let's check:
I'll ask only for particle output, once every quarter time unit:
Bob: Yes, we'll get to graphics soon. But let's do some real lab bench
work here. Ah! You see, at time 1.25 the separation of the particles is
clearly smaller than at other times. That must have been the periastron
passage, roughly. So the period of the orbit must be 2.5, give or take.
11.1. Starting Again
|gravity> ruby test.rb < euler.in
dt = 0.01
dt_dia = 1
dt_out = 1
dt_end = 1
at time t = 0, after 0 steps :
E_kin = 0.125 , E_pot = -1, E_tot = -0.875
E_tot - E_init = 0
(E_tot - E_init) / E_init =-0
at time t = 1, after 100 steps :
E_kin = 0.838 , E_pot = -1.7, E_tot = -0.867
E_tot - E_init = 0.00822
(E_tot - E_init) / E_init =-0.0094
1.0000000000000000e+00
4.4322956434140903e-01 3.8421555868663582e-01
-1.2943653128939152e+00 2.5812000666903590e-02
Alice: Did you set this up? A relative energy accuracy of
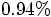 , very close!
, very close!
11.2. Linear Scaling
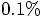 now. Let's see.
now. Let's see.
|gravity> ruby test.rb < euler.in
dt = 0.001
dt_dia = 1
dt_out = 1
dt_end = 1
at time t = 0, after 0 steps :
E_kin = 0.125 , E_pot = -1, E_tot = -0.875
E_tot - E_init = 0
(E_tot - E_init) / E_init =-0
at time t = 1, after 1000 steps :
E_kin = 0.864 , E_pot = -1.74, E_tot = -0.874
E_tot - E_init = 0.000825
(E_tot - E_init) / E_init =-0.000943
1.0000000000000000e+00
4.3302178053157708e-01 3.7860453335416983e-01
-1.3147926449876397e+00 7.1843385614138713e-03
Alice: Almost too good: the relative error is now
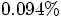 .
It has decreased by the predicted factor ten. Let's do this:
.
It has decreased by the predicted factor ten. Let's do this:
|gravity> ruby test.rb < euler.in
dt = 1.0e-05
dt_dia = 1
dt_out = 1
dt_end = 1
at time t = 0, after 0 steps :
E_kin = 0.125 , E_pot = -1, E_tot = -0.875
E_tot - E_init = 0
(E_tot - E_init) / E_init =-0
at time t = 1, after 100000 steps :
E_kin = 0.867 , E_pot = -1.74, E_tot = -0.875
E_tot - E_init = 8.25e-06
(E_tot - E_init) / E_init =-9.43e-06
1.0000000000000000e+00
4.3186966438051116e-01 3.7796470836807455e-01
-1.3171480879236508e+00 5.0327840503739613e-03
Bob: And indeed the error comes down by a factor of a hundred. Note that
the integrator halts after exactly 100,000 steps, not one more and not one
less. Yesterday evening, when I tried it out, it kept overshooting to
100,001 steps, so that was why I added that extra half step in the halting
criteria.
11.3. A Full Orbit
|gravity> ruby test.rb < euler.in
dt = 0.01
dt_dia = 2.5
dt_out = 10
dt_end = 10
at time t = 0, after 0 steps :
E_kin = 0.125 , E_pot = -1, E_tot = -0.875
E_tot - E_init = 0
(E_tot - E_init) / E_init =-0
at time t = 2.5, after 250 steps :
E_kin = 0.936 , E_pot = -0.54, E_tot = 0.395
E_tot - E_init = 1.27
(E_tot - E_init) / E_init =-1.45
at time t = 5, after 500 steps :
E_kin = 0.603 , E_pot = -0.209, E_tot = 0.394
E_tot - E_init = 1.27
(E_tot - E_init) / E_init =-1.45
at time t = 7.5, after 750 steps :
E_kin = 0.529 , E_pot = -0.135, E_tot = 0.394
E_tot - E_init = 1.27
(E_tot - E_init) / E_init =-1.45
at time t = 10, after 1000 steps :
E_kin = 0.495 , E_pot = -0.101, E_tot = 0.394
E_tot - E_init = 1.27
(E_tot - E_init) / E_init =-1.45
1.0000000000000000e+00
7.6937453936571965e+00 -6.2777200566159870e+00
8.1220683064181454e-01 -5.7420020123998905e-01
Alice: That's funny, a large energy error right away and then the energy
seems to be frozen in.
11.4. Zooming In
|gravity> ruby test.rb < euler.in
dt = 0.01
dt_dia = 0.5
dt_out = 10
dt_end = 2.5
at time t = 0, after 0 steps :
E_kin = 0.125 , E_pot = -1, E_tot = -0.875
E_tot - E_init = 0
(E_tot - E_init) / E_init =-0
at time t = 0.5, after 50 steps :
E_kin = 0.231 , E_pot = -1.1, E_tot = -0.872
E_tot - E_init = 0.0033
(E_tot - E_init) / E_init =-0.00377
at time t = 1, after 100 steps :
E_kin = 0.838 , E_pot = -1.7, E_tot = -0.867
E_tot - E_init = 0.00822
(E_tot - E_init) / E_init =-0.0094
at time t = 1.5, after 150 steps :
E_kin = 3.37 , E_pot = -2.95, E_tot = 0.417
E_tot - E_init = 1.29
(E_tot - E_init) / E_init =-1.48
at time t = 2, after 200 steps :
E_kin = 1.26 , E_pot = -0.865, E_tot = 0.398
E_tot - E_init = 1.27
(E_tot - E_init) / E_init =-1.45
at time t = 2.5, after 250 steps :
E_kin = 0.936 , E_pot = -0.54, E_tot = 0.395
E_tot - E_init = 1.27
(E_tot - E_init) / E_init =-1.45
Alice: So the disaster happened between a time of 1 and 1.5. That must
have been when the first pericenter passage occurred, the place where
the particles made their closest approach during one orbit.
11.5. Pericenter Passage
|gravity> ruby test.rb < euler.in
dt = 0.01
dt_dia = 10
dt_out = 0.25
dt_end = 1.5
at time t = 0, after 0 steps :
E_kin = 0.125 , E_pot = -1, E_tot = -0.875
E_tot - E_init = 0
(E_tot - E_init) / E_init =-0
1.0000000000000000e+00
9.6984896296142042e-01 1.2383206879933301e-01
-2.5280864394541708e-01 4.8458243922783906e-01
1.0000000000000000e+00
8.7455226567482147e-01 2.3948976867782423e-01
-5.2597914456085060e-01 4.3083603675399151e-01
1.0000000000000000e+00
7.0559656638283363e-01 3.3480149737403997e-01
-8.5114538471899592e-01 3.1158537532636715e-01
1.0000000000000000e+00
4.4322956434140903e-01 3.8421555868663582e-01
-1.2943653128939152e+00 2.5812000666903590e-02
1.0000000000000000e+00
4.3573377318392045e-02 2.9481575851334291e-01
-1.9466715027999648e+00 -1.1087280827004695e+00
1.0000000000000000e+00
-1.1742854070954888e-01 -3.1759379188140036e-01
1.2444634633070424e+00 -2.2783744800811112e+00
Alice: This is sure hard to read. It is definitely time to get some form
of graphics going. This must be how people analyzed the first N-body
calculations, in the sixties!