12. Analytical Checks
Alice: You know, we really should be able to derive the orbital period
analytically. Let me try to remember my celestial mechanics. I remember
that there was one equation that had no factors of
Bob: That's a handy formula to remember. What does that give in our
case? We started with
Alice: We'll have to reconstruct that. It must be larger than 0.5, but
not much larger. At the time of pericenter the particles were much closer
than at apocenter, which means that the eccentricity was fairly large,
and the apocenter distance not much smaller than
I remember another handy formula: the total energy in a two-body system
is equal to
Bob: I can see that it is useful to remember those qualitative facts.
That is easier than trying to remember factors of 3 or 4 in formulas that
you learn by heart and than later half forget.
Alice: Yes, the only numbers I like are 1 and 0 and infinity. So let
us determine the total energy, and then we now our semi-major axis
Bob: But we have that already: according to the output of my program
it is E_tot = -0.875, initially. In other words,
Alice: Inverting my previous equation, we get
Bob: That is puzzling. But you just stepped through my code. You
were so happy with the clarity of the statements like
etot = ekin + epot.
Alice: Let's do an independent check. This is like debugging, but
now on the level of the physics, rather than the numerics. Let me just
use pen and paper to determine the initial total energy. Here are the
equations:
Bob: Right. And these are velocities in the center of mass frame
of the two particles. These are equal in magnitude but opposite in
direction, so each one is one half of the relative velocity. The
original relative velocity was 1/2, so each of the two is 1/4, and
Bob: If this is right, then the question is what went wrong with my
program? I agree that a value of
Alice: Well, your calculation can't be all wrong. You had the factor
7 in the denominator, that's unlikely to come out correctly by chance.
You were off by a factor 4. I think there must be something wrong with
your units.
Bob: My units??? You saw as well as I did that I used
Hey, wait a minute. We use a mass of 1 for our relative particle
and a mass of 0.5 for each individual particle. There is a factor
two between them, and two times two makes four.
Alice: Indeed, the factor four that your program was off with.
And I think you found the solution, or at least the direction of the
solution. Look, in your code you use the correct scaling for kinetic
and potential energy, but you don't have any mass factors in there.
Bob: Perhaps I was thinking about the fact that we started with a
total mass of one, or perhaps I just forgot. Can we correct that?
The potential energy is
Alice: Problem solved.
Bob: Still, I wonder, I thought I had done something similar in another
code, quite a while ago, and I think I did give that one considerable
thought. The question is, should I do my energy diagnostics in the
center of mass frame, or is there a way to save my current code?
What I mean is that the whole two-body problem is specified in terms
of relative positions and relative velocities and the sum of the masses.
In the equations of motions, nowhere do the individual velocities in
the center of mass frame come in, nor do the individual masses appear.
That makes me think that my mistake might not have been that bad after
all. Could it be that I am always off by a constant factor, or at
least by the same factor in potential and kinetic energy, so that it
still makes sense to add the two and thus check for energy conservation?
Alice: What we have to do is to check how the reduced mass comes in.
Bob: Ah yes, that rings a bell, from my celestial mechanics class.
The relative motion of two bodies under the influence of gravity, or
of electrostatic forces for that matter, can be described by the
equivalent motion of a pseudo-particle with a different mass, the
reduced mass. But how did that go? We can look in any old celestial
mechanics book, but it would be more fun to try to reconstruct it
ourselves.
12.1. Celestial Mechanics
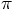 or
whatever in it. Ah yes,
or
whatever in it. Ah yes,

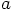 is the semi-major axis,
is the semi-major axis, 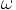 is the
angular frequency of the motion, in other words the period of the
orbit is given in terms of
is the
angular frequency of the motion, in other words the period of the
orbit is given in terms of 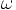 as
as 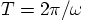 .
.
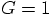 and took
and took 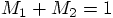 but what was our initial value for
but what was our initial value for 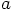 ?
?
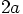 .
.

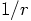 happens to be
happens to be 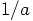 .
.
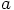 .
.
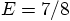 .
.

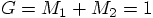 , we get
, we get

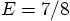 ,
that gives us
,
that gives us 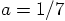 . But hey, that can't be right. It
should be larger than 0.5, since the maximum distance between two particles
in any Kepler orbit is
. But hey, that can't be right. It
should be larger than 0.5, since the maximum distance between two particles
in any Kepler orbit is 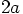 , and we started at a distance of
unity!
, and we started at a distance of
unity!
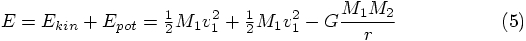
 and
and  , right?
, right?
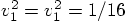 . Let's do it very carefully, to
make sure we don't drop some factor somewhere. We have now for the
initial total energy:
. Let's do it very carefully, to
make sure we don't drop some factor somewhere. We have now for the
initial total energy:
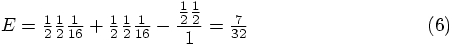

|gravity> bc -lq
4/7
.57142857142857142857
This has to be correct. We did it from first principles, little step
for little step, and the result is just what was expected.
12.2. The Role of the Masses
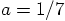 is unphysical.
But like I said, you just checked with me every statement in the code!
is unphysical.
But like I said, you just checked with me every statement in the code!
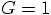 ,
and there were no other scaling units involved. We gave each particle
a mass of 0.5, with a total mass of 1.0, which went into the Body
description for the relative motion of the two particles.
,
and there were no other scaling units involved. We gave each particle
a mass of 0.5, with a total mass of 1.0, which went into the Body
description for the relative motion of the two particles.

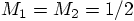 , so neglecting the mass
factors, I have overestimated the potential energy by a factor of four.
The kinetic energy is
, so neglecting the mass
factors, I have overestimated the potential energy by a factor of four.
The kinetic energy is


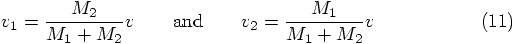
 is still the relative velocity between the two particles.
is still the relative velocity between the two particles.
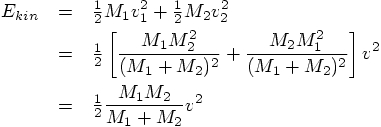
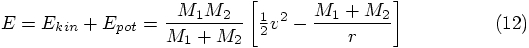

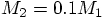 , for example,
, for example, 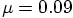 ,
to within about ten percent the same as the mass of the light particle.
Most of the relative motion also occurs in the motion of the light particle,
so in the limit that the mass ratio grows even much larger, the relative
motion becomes effectively that of the light particle around a fixed center
of attraction.
,
to within about ten percent the same as the mass of the light particle.
Most of the relative motion also occurs in the motion of the light particle,
so in the limit that the mass ratio grows even much larger, the relative
motion becomes effectively that of the light particle around a fixed center
of attraction.
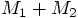 factor to my potential energy.
If in the future we or someone else will use our code for a case where
the sum of the masses is not unity, the code as it is will give a wrong
answer.
factor to my potential energy.
If in the future we or someone else will use our code for a case where
the sum of the masses is not unity, the code as it is will give a wrong
answer.