2. Integrators on the Menu
Bob: It will be easy to show you what I have done, in order to
implement the leapfrog. My first attempt was to code it up in the
same way as we did for the forward Euler scheme. Remember how we
did that? In order to take one forward Euler step, we used the
following method:
Bob: Yes, they are much more convenient; the first set defined the
velocities at half-step times, but here everything is defined at the
same time: positions, velocities, and accelerations.
Alice: Why did you not start by implementing the first equation first?
Bob: If I would step forward the position first, I would not be able
to obtain the acceleration
Alice: Can you summarize that in a list of steps?
Bob: Here is my recipe:
Alice: Ah, I see now. You really had to add
The only drawback of writing it in such a compact and smart way is
that the correspondence between the equations is not immediately
clear, when you look at the code.
Bob: You could call it FORMula TRANslating with an optimizer.
Alice: You may want to write a version where you switch off your
clever optimizer. Let's see whether we can translate your equations
more directly:
Bob: But it introduces an extra variable, so there is a trade off.
Yes, that would be fine as well. It depends on what you find more elegant.
In fact, note that none of these methods are very efficient. At the
beginning of the next step, we will calculate the old acceleration,
which is the same as what was called the new acceleration in the
previous step. So while we are stepping along, we do every
acceleration calculation twice, in your version as well as in mine.
I was thinking about avoiding that redundancy, but I realized that
that would make the code less clear. And as long as we are integrating
only two bodies, there is really no need to optimize at this point.
Alice: That reminds me of Alan Perlis' saying: ``premature optimization
is the root of all evil''.
Bob: I thought that quote was from Hoare, the inventer of qsort; I came
across it in some of the writings of Knuth.
Alice: It is probably a sign of a a good idea that it gets attributed to
different people.
Bob: But every good idea has to be used sparingly. Postponing optimization
too long will never grow fruit.
Alice: Did you just make that up?
Bob: I just thought about balancing roots and fruits, as a warning
against too much abstraction, modularity, cleanliness, and all that
stands in the way of optimized code. But for now, as long as we are
still working on a toy project, I really don't mind.
Alice: You have told us how you wrote your first leapfrog version of
evolve_step; and now I can see what you did in the much more condensed
version in your code:
Instead of repeating the three line calculation of the acceleration twice
you put in into a method instead:
Another nice example of a method without parameters, like the ekin
and epot that we saw before.
Bob: I know you would like that. I'm curious, how would your version
of the leapfrog look, in this notation? You start by introducing variables
old_acc and new_acc, so that must then become:
Alice: That is interesting, isn't it? At first I really preferred my
version, both because it was shorter and because it remained closer to
the mathematical formulae that you had written down. But I must admit
that I like the way you encapsulated -- dare I say modularized -- the
acceleration into a separate method. And now suddenly my version looks
a bit clumsy and lengthy.
Bob: But I'm glad we're going over the code so carefully together.
I wouldn't have thought about your way of writing the leapfrog, and
it is nice to try different variations, in order to see which one you
like best.
Alice: So I agree: we'll stick with yours. And your forward Euler now
also looks very short.
Bob: In fact, my first try was even one line shorter:
I like this form! What is wrong with it? You're not the type of
person who likes to add an extra line without a good reason!
Bob: It is totally wrong. But it took me quite a while to figure
that out. Can you guess what is wrong?
Alice: It looks right to me. In fact, it is classic forward Euler.
The position gets increased by the velocity times time step, and the
velocity gets increased by the acceleration times time step. What
can be wrong with that?
Bob: Let me give you a hint. You praised the symmetry of the two lines.
But are they really symmetric?
Alice: Is that a trick question? In both lines literally all characters
are the same, except that pos above is replaced by its derivative vel
below, and vel above is also replaced by its derivative acc below.
Bob: And in both cases the left-hand side of the equation contains an
instance variable, and the right-hand side contains a method . . .
Alice: Yes, I had already commented on that, praising you! The left hand
side is symmetric, because the variable holding @vel is exactly of
the same sort of thing as the variable holding @pos. How much
further do you want to push me to spell everything out? Okay. The right
hand side is symmetric, because the method acc . . .
Bob: You see! I can see from your face that you got it.
Alice: Well, now that is a subtle bug. What a beauty!
Bob: Yeah, I agree, I first felt rather stupid, but now that I see your
reaction, I think that I may have stumble upon an interesting variation
of stupidity.
Alice: I can't wait to show this to the students, and let them figure
it out.
Bob: In a class full of them, there may be a few that get it quicker
than we did.
Alice: So much the better, more power to them! What a tricky situation.
So yes, thanks to your prodding I saw it all as in a flash. They two lines
are not symmetric. In the first line, vel just reads out a stored
value, while in the second line, acc computes a value on the fly. And it
does so using the pos value at that time, a value that has just been
changed prematurely in the previous line. So the velocity increment
will be wrong! And what is worse, you can't repair the damage by changing
the order of the two lines:
Bob: So I had to add a third line, introducing a temporary variable,
old_acc, the acceleration at the beginning of the step.
Alice: I'm impressed that you found this bug at all.
Bob: Well, if you stare at something long enough, chances are that you
stumble upon a moment of clarity.
Alice: But no guarantee. And even testing would not have revealed that
bug, since the bug introduces a second-order error, and the error in a
first-order method is second-order anyway. To be explicit, in the last
version, the position increment would use a velocity value vel that
would be off by an amount proportional to dt, so the product vel*dt
would introduce an error in @pos that would be proportional to
dt*dt. So the method would still be first-order accurate!
Bob: But it would no longer be a forward Euler method. Yes, it is tricky.
It makes you wonder how many hidden bugs there are still lurking in
even well-tested codes, let alone the many codes that are not-so-well
tested . . .
Alice: Back to your two integrator methods. I very much like the idea
of separating out the acceleration as a calculation that gets done in
a separate method. But where is the magic that enables you to call
the shots, when you call evolve? How does evolve know that a first
argument of the string "forward" directs it to execute the
method forward, and similarly that a first argument of the string
"leapfrog" directs it to execute the method leapfrog?
Bob: That happens through the send method.
Alice: Another piece of Ruby magic, I take it. But how does it work?
It seems too easy, though. You send the integration method on its way?
Bob: send is a method that comes with each object in Ruby. It is
one of the general methods that each object inherits as soon as it is
created. What send does is to call another method. send first
reads the name of the other method from the string in its first argument,
and then it passes its remaining arguments to the other method. So in
our case send("leapfrog", dt), for example amounts to the
same as giving the command leapfrog(dt) directly.
Alice: That's really nice. Clearly, the designer of Ruby had a very
good sense of what is needed to built a truly flexible language. What
is his name?
Bob: Matsumoto. I don't know much about him, but yes, he clearly
knows how to create a clean yet powerful language.
Alice: I'd like to meet him someday. Does he live in Japan?
Bob: He does.
Alice: Well, there are many astronomy conferences in Japan, so I hope
I'll get a chance, some day. And if we really get to build a nice toy
model in Ruby, he may enjoy playing with stars.
Bob: Now that you see how I have extended our Body class with a menu
of integrators, would you like to see it all in action?
Alice: Sure. Let's try the hard case again, for ten time units. That
seemed to take forever with the forward Euler method. Let's try it for
a few time steps, both with forward Euler and with leapfrog.
2.1. The Leapfrog Method
def evolve_step(dt)
r2 = @pos*@pos
r3 = r2*sqrt(r2)
acc = @pos*(-@mass/r3)
@pos += @vel*dt
@vel += acc*dt
end
Switching to the leapfrog, I wrote:
def evolve_step(dt)
r2 = @pos*@pos
r3 = r2*sqrt(r2)
acc = @pos*(-@mass/r3)
@vel += acc*0.5*dt
@pos += @vel*dt
r2 = @pos*@pos
r3 = r2*sqrt(r2)
acc = @pos*(-@mass/r3)
@vel += acc*0.5*dt
end
Alice: I presume you used the second set of equations which you
wrote before:
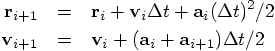
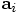 that is needed for the
second equation, since the acceleration at time i can only be obtained
from the position at time i. Therefore, the first thing to do is to
obtain
that is needed for the
second equation, since the acceleration at time i can only be obtained
from the position at time i. Therefore, the first thing to do is to
obtain 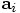 . Only then can I step forward the position,
in order to calculate
. Only then can I step forward the position,
in order to calculate 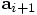 . However, before doing
that, I'd better use the old acceleration
. However, before doing
that, I'd better use the old acceleration 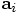 , since
another acceleration call that would calculate
, since
another acceleration call that would calculate 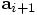 would overwrite
would overwrite 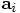 .
.
2.2. Two Different Versions
So the `leap' part of the frog shows itself in this half step
business for the velocity.
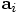
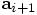
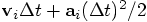 to the position
in the third of your five steps. But since you had already updated
the velocity from
to the position
in the third of your five steps. But since you had already updated
the velocity from 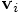 to effectively
to effectively
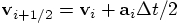 , you could
abbreviate the position update. You just added
, you could
abbreviate the position update. You just added
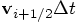 to the position instead. Clever!
to the position instead. Clever!
def evolve_step(dt)
r2 = @pos*@pos
r3 = r2*sqrt(r2)
old_acc = @pos*(-@mass/r3)
@pos += @vel*dt + old_acc*0.5*dt*dt
r2 = @pos*@pos
r3 = r2*sqrt(r2)
new_acc = @pos*(-@mass/r3)
@vel += (old_acc + new_acc)*0.5*dt
end
Hey, it is even one line shorter than what you wrote!
2.3. Tidying Up
def leapfrog(dt)
@vel += acc*0.5*dt
@pos += @vel*dt
@vel += acc*0.5*dt
end
def acc
r2 = @pos*@pos
r3 = r2*sqrt(r2)
@pos*(-@mass/r3)
end
def leapfrog(dt)
old_acc = acc
@pos += @vel*dt + old_acc*0.5*dt*dt
new_acc = acc
@vel += (old_acc + new_acc)*0.5*dt
end
So there: one line longer than my version, and with longer lines to boot.
2.4. A Subtle Bug
def forward(dt)
old_acc = acc
@pos += @vel*dt
@vel += old_acc*dt
end
def forward(dt)
@pos += vel*dt
@vel += acc*dt
end
Alice: That looks beautifully symmetric. I see that you left out
the @ sign at the right in front of vel; it doesn't make
a difference, since vel is a method returning @vel anyway,
and this way the symmetry between the two lines comes out better.
def forward(dt)
@vel += acc*dt
@pos += vel*dt
end
In that case, the velocity gets updated correctly, with the
acceleration based on the old @pos value, but now the
position increment gets wrongly calculated, since it uses the new
value for vel, while I should have used the old. A lose-lose
situation, whatever order you give these two lines.
2.5. Ordering an Integrator
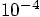 , while the next-to-last run already had an energy
accuracy of a few time
, while the next-to-last run already had an energy
accuracy of a few time 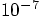 .
.
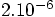 , while the
difference between the previous run and the run before that was
, while the
difference between the previous run and the run before that was
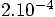 . So the scheme really is second-order accurate.
Still, it would be nice to try another second order integrator, one
that does not have built-in energy conservation.
. So the scheme really is second-order accurate.
Still, it would be nice to try another second order integrator, one
that does not have built-in energy conservation.