3. Runge Kutta
Alice: Good morning, Bob! Any luck with extending your menu of
integrators?
Bob: Yes, I added two Runge-Kutta integrators, one second-order
and one fourth-order in accuracy. The changes are again minimal.
For the driver program there is no change at all. The only difference
is that you can now call evolve with method = "rk2" to
invoke the second-order Runge-Kutta integrator, or "rk4" for
the fourth-order integrator.
Here are the additions to the Body class:
Alice: Even the fourth-order method is quite short. But let me first
have a look at your second-order Runge-Kutta. I see you used an
old_pos just like I used an old_acc in my version of
the leapfrog.
Bob: Yes, I saw no other way but to remember some variables before they
were overwritten.
Alice: My numerical methods knowledge is quite rusty. Can you remind me
of the idea behind the Runge-Kutta algorithms?
Bob: The Runge-Kutta method does not leap, as the leapfrog does. It is
more careful. It feels its way forward by a half-step, sniffs out the
situation, returns again, and only then it makes a full step, using the
information gained in the half-step.
Alice: Like a cat?
Bob: Do cats move that way?
Alice: Sometimes, when they are trying to catch a mouse, they behave
as if they haven't seen their prey at all. They just meander a bit,
and then return, so that the poor animal thinks that it is safe now.
But then, when the mouse comes out of hiding, the cat pounces.
Bob: So we should call the Runge-Kutta method the leapcat method?
Alice: Why not?
Bob: I'm not sure. For one thing, my code doesn't meander. You can tell
your students what you like, I think I'll be conservative and stick to Runge
Kutta.
Here are the equations that incorporate the idea of making a half-step
first as a feeler:
Alice: Ah yes, now it is very clear how you use the information from the
half-step, in the form of the velocity and acceleration there, to improve
the accuracy of the full step you take at the end.
Bob: Wait a minute. Looking again at the equations that I got from a
book yesterday, I begin to wonder. Is this really different from the
leapfrog method? We have seen that you can write the leapfrog in at
least two quite different ways. Perhaps this is a third way to write it?
Alice: I think it is different, otherwise it would not have a different
name, but it is a good idea to check for ourselves. Let us write out the
effect of the equations above, by writing the half-step values in
terms of the original values. First, let's do it for the position:
Bob: Hey, that is the exact same equation as we had for the leapfrog.
Now I'm curious what the velocity equation will tell us.
Ah, that doesn't work, we cannot write
Alice: You are right. So the two methods are really different then.
Good to know. Still, let us see how different they are. The
corresponding equation for the leapfrog is:
Bob: Ah, that is neat. The Leapfrog velocity jump uses the average
acceleration, averaged between the values at the beginning and at the
end of the leap. The Runge-Kutta method approximates this average
by taking the midpoint value.
Alice: Or putting it the other way around, the leapfrog approximates
the midpoint value by taking the average of the two accelerations.
Bob: Yes, you can look at it both ways. In fact, if you take your view,
you can see that the leapfrog is twice as efficient as Runge-Kutta, in that
it calculates only the accelerations at the integer time points. In
contrast, the Runge-Kutta method also calculates the accelerations at the
half-integer points in time. So it requires twice as many acceleration
calculations.
Of course, in my current code that is not obvious, since I am calculating
the acceleration twice in the leapfrog as well. However, it would be easy
to rewrite it in such a way that it needs only one acceleration calculation.
And in the Runge-Kutta method you cannot do that.
Alice: Going back to the original equations you wrote down for your
second-order Runge-Kutta code:
I must admit that your way of coding them up is not immediately transparent
to me. If I had to implement these equations, I would have written something
like:
Bob: Yes, that is how I started as well. But then I realized that
I could save three lines by writing them the way I did in the code:
The number of times you calculate the acceleration is the same, but
instead of introducing five new variables, I only introduced two.
Alice: it is probably a good idea to show both ways to the students,
so that the whole process of coding up an algorithm becomes more
transparent to them.
Bob: Yes, I'll make sure to mention that to them.
Alice: Since we know now that the two methods are different, it seems
likely that the energy conservation in the Runge-Kutta method is a
better indicator for the magnitude of the positional errors than it
was in the leapfrog case. Shall we try the same values as we used
before, but now for the Runge-Kutta method?
Bob: I'm all for it! Let me call the file integrator_driver2.rb:
Alice: That is interesting. I guess you could say that the errors of a
second-order integrator are only guaranteed to be smaller than something
that scales like the square of the time step, but still, this is a bit
mysterious. Shall we shrink the time step by another factor of ten?
3.1. Two New Integrators
3.2. A Leapcat Method
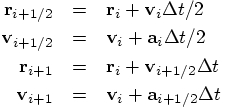
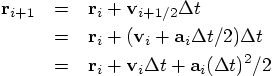
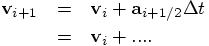
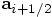 in terms of quantities at times
in terms of quantities at times 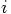 and
and 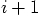 .
It really is a new result, computed halfway.
.
It really is a new result, computed halfway.
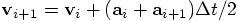
3.3. Translating Formulas Again
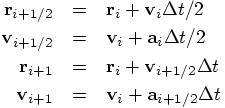
def rk2(dt)
old_pos = pos
old_vel = vel
half_pos = pos + vel*0.5*dt
half_vel = vel + acc*0.5*dt
@pos = half_pos
half_acc = acc
@vel = old_vel + half_acc*dt
@pos = old_pos + half_vel*dt
end
Note that I first move the position variable pos from
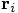 to
to 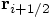 in
the fifth line of this method. Or more precisely: I assign
the value of
in
the fifth line of this method. Or more precisely: I assign
the value of 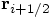 to the variable pos.
I then invoke the method acc on
to the variable pos.
I then invoke the method acc on 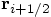 in order to obtain
in order to obtain 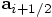 , the value of
which I then assign to the variable half_acc.
, the value of
which I then assign to the variable half_acc.
3.4. Energy Conservation
|gravity> ruby integrator_driver2a.rb < euler.in
dt = 0.001
dt_dia = 10
dt_out = 10
dt_end = 10
method = rk2
at time t = 0, after 0 steps :
E_kin = 0.125 , E_pot = -1 , E_tot = -0.875
E_tot - E_init = 0
(E_tot - E_init) / E_init =-0
at time t = 10, after 10000 steps :
E_kin = 0.555 , E_pot = -1.43 , E_tot = -0.875
E_tot - E_init = 6.02e-05
(E_tot - E_init) / E_init =-6.88e-05
1.0000000000000000e+00
5.9856491479183715e-01 -3.6183772788952318e-01
1.0319067591346045e+00 2.1153690796461602e-01
Alice: An energy error of order several time 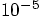 ,
that is more than a hundred times worse than we saw for the leapfrog,
where we had an error of a few times
,
that is more than a hundred times worse than we saw for the leapfrog,
where we had an error of a few times 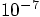 , for the
same time step value. Let's try a ten times smaller time step:
, for the
same time step value. Let's try a ten times smaller time step:
|gravity> ruby integrator_driver2b.rb < euler.in
dt = 0.0001
dt_dia = 10
dt_out = 10
dt_end = 10
method = rk2
at time t = 0, after 0 steps :
E_kin = 0.125 , E_pot = -1 , E_tot = -0.875
E_tot - E_init = 0
(E_tot - E_init) / E_init =-0
at time t = 10, after 100000 steps :
E_kin = 0.554 , E_pot = -1.43 , E_tot = -0.875
E_tot - E_init = 6.06e-08
(E_tot - E_init) / E_init =-6.92e-08
1.0000000000000000e+00
5.9961087073768127e-01 -3.6064562545351836e-01
1.0308109943449486e+00 2.1387625542844693e-01
Bob: That is a surprise: the energy error has become a thousand times
smaller, instead of a hundred. The Runge-Kutta seems to behave as if
it is a third-order method, rather than a second order method.
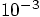 , where we had
, where we had 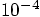 for the leapfrog. So the Runge-Kutta, for a time step of 0.001, is a
hundred times worse in energy conservation and ten times worse in the
accuracy of the positions, compared with the leapfrog. Then, at a
time step of 0.0001, the energy error lags only a factor ten behind
the leapfrog. Okay, let's go to a time step of 0.00001:
for the leapfrog. So the Runge-Kutta, for a time step of 0.001, is a
hundred times worse in energy conservation and ten times worse in the
accuracy of the positions, compared with the leapfrog. Then, at a
time step of 0.0001, the energy error lags only a factor ten behind
the leapfrog. Okay, let's go to a time step of 0.00001:
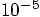 ,
as we can now see by comparison with the third run. That is strange.
The positional accuracy increases by a factor 100, yet the energy accuracy
increases by a factor 1000.
,
as we can now see by comparison with the third run. That is strange.
The positional accuracy increases by a factor 100, yet the energy accuracy
increases by a factor 1000.
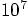 integration steps, I'm surprised we got even that far. At each time,
round off errors must occur in the calculations that are of order
integration steps, I'm surprised we got even that far. At each time,
round off errors must occur in the calculations that are of order
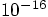 . Then statistical noise in so many calculations
must be larger than that by at least the square root of the number of
time steps, or
. Then statistical noise in so many calculations
must be larger than that by at least the square root of the number of
time steps, or 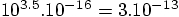 .
.
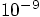 . Once more a factor a hundred more accurate than
the difference between the previous two integrations. Clearly the
positional accuracy of the second order Runge-Kutta is second-order
accurate, like that of the leapfrog.
. Once more a factor a hundred more accurate than
the difference between the previous two integrations. Clearly the
positional accuracy of the second order Runge-Kutta is second-order
accurate, like that of the leapfrog.