./ch06.html

ToC

6.1. A Multiple leapfrog

Alice: Hi, Bob! To judge from the look on your face, I would bet you found a good recipe for a sixth-order Runge Kutta method.

Bob: As a matter of fact, yes, I did. But before I show it to you, let me know, did you find out the history behind the mysterious formula in Abramowitz and Stegun, that we have been sweating over so much?

Alice: Yes, indeed. It was presented in 1925 by a Finnish mathematician, in a Finnish publication. Here is the full reference: Nystrom, E.J., 1925, Acta Soc. Sci. Fenn., 50, No.13, 1-55. I dug it up in the library.

Bob: I'm impressed! I hope it was not written in Finnish?

Alice: No, it was written in German.

Bob: That wouldn't have helped me.

Alice: Fortunately, I had some German in high school, and I remembered just enough to figure out the gist of the story.

Bob: But how did you find this article?

Alice: I first went to some text books on numerical methods. After some searching, I learned that our mystery formula is an example of what are called Runge-Kutta-Nystrom algorithms. It was Nystrom who made the extension from normal Runge-Kutta methods to special treatments for second-order differential equations. And there is a whole lot more to the history. In recent years, quite a number of interesting books have appeared that have a bearing on the general topic. I found it hard to put them down.

Bob: Now that you got bitten by the bug, perhaps you'll be deriving new methods for us, from scratch?

Alice: It's tempting to do so, just to see how it's done. Like having a peak into the kitchen, rather than ordering from a menu. But not now.

Bob: No, let me show you first what I found on my menu, a Japanese menu it turned out, which featured a sixth-order Runge-Kutta method prepared by an astronomer working at the National Observatory in Tokyo, Haruo Yoshida.

Alice: Let me guess how long the code will be. The rk2 method was five lines long, and the rk4 method was eight lines long. I seem to remember that the complexity of Runge-Kutta methods increases rapidly with order, so the new code must at least be twice as long, more likely a bit more. Okay, I'll bet on twenty lines.

Bob: How much are you willing to bet?

Alice: I'm not much of a gambler. Let's say you'll get my admiration if you did it in less than twenty lines.

Bob: How much admiration will I get if it would be less than ten lines?

Alice: I don't know, since I wouldn't believe you.

Bob: It that case you must be ready for a really wild move. How much are you willing to bet against my having written a sixth-order Runge-Kutta code in five lines?

Alice: Hahaha! I will bet a good laugh. You can't be serious.

Bob: I am.

Alice: Huh? You're not going to tell me that your sixth-order Runge-Kutta is as long as the second-order Runge-Kutta?

Bob: Seeing is believing. Here it is, in the file yo6body.rb

   def yo6(dt)
     d = [0.784513610477560e0, 0.235573213359357e0, -1.17767998417887e0,
          1.31518632068391e0]
     for i in 0..2 do leapfrog(dt*d[i]) end
     leapfrog(dt*d[3])
     for i in 0..2 do leapfrog(dt*d[2-i]) end
   end

Alice: Seven leapfrog calls? And that does it?

Bob: Yes, that does it, or so is the claim. It was invented by Yoshida, a Japanese astronomer, around 1990, that's why I called it yo6 instead of rk6. I haven't gotten the time to test it out yet. I just finished it when you came in.

6.2. Great!

Alice: I'm not sure whether to call this incredible, shocking, or what. But before I look for the right adjective, let me first see that it does what you claim it does.

Bob: I'm curious too. Let us take our good old Kepler orbit for a spin: ten time units, as before. We will start with the fourth-order Runge-Kutta method:

 |gravity> ruby integrator_driver2g.rb < euler.in
 dt = 0.001
 dt_dia = 10
 dt_out = 10
 dt_end = 10
 method = rk4
 at time t = 0, after 0 steps :
   E_kin = 0.125 , E_pot =  -1 , E_tot = -0.875
              E_tot - E_init = 0
   (E_tot - E_init) / E_init =-0
 at time t = 10, after 10000 steps :
   E_kin = 0.554 , E_pot =  -1.43 , E_tot = -0.875
              E_tot - E_init = -2.46e-09
   (E_tot - E_init) / E_init =2.81e-09
   1.0000000000000000e+00
   5.9961758437074986e-01 -3.6063455639926667e-01
   1.0308068733946525e+00  2.1389536225475009e-01

for which we found this reasonable result, with a relative accuracy in the conservation of the total energy of a few in a billion. Presumably the sixth-order method should do significantly better, for the same time step value:

 |gravity> ruby integrator_driver3a.rb < euler.in
 dt = 0.001
 dt_dia = 10
 dt_out = 10
 dt_end = 10
 method = yo6
 at time t = 0, after 0 steps :
   E_kin = 0.125 , E_pot =  -1 , E_tot = -0.875
              E_tot - E_init = 0
   (E_tot - E_init) / E_init =-0
 at time t = 10, after 10000 steps :
   E_kin = 0.554 , E_pot =  -1.43 , E_tot = -0.875
              E_tot - E_init = 1.72e-14
   (E_tot - E_init) / E_init =-1.97e-14
   1.0000000000000000e+00
   5.9961755487188750e-01 -3.6063458346955279e-01
   1.0308069102782800e+00  2.1389530415211538e-01

6.3. Too Good?

Alice: Significant, all right: almost machine accuracy. Can you give a larger time step? Make it ten times as large! That may be way too large, but we can always make it smaller again.

Bob: My pleasure!

 |gravity> ruby integrator_driver3b.rb < euler.in
 dt = 0.01
 dt_dia = 10
 dt_out = 10
 dt_end = 10
 method = yo6
 at time t = 0, after 0 steps :
   E_kin = 0.125 , E_pot =  -1 , E_tot = -0.875
              E_tot - E_init = 0
   (E_tot - E_init) / E_init =-0
 at time t = 10, after 1000 steps :
   E_kin = 0.554 , E_pot =  -1.43 , E_tot = -0.875
              E_tot - E_init = 1.23e-14
   (E_tot - E_init) / E_init =-1.41e-14
   1.0000000000000000e+00
   5.9960497793690160e-01 -3.6065834429401844e-01
   1.0308122043933747e+00  2.1385575804694398e-01

Alice: No! This is too good to be true. Still essentially machine accuracy, for only a thousand steps, while rk2 with ten-thousand steps did far worse, by a whopping factor of a hundred thousand. Well, let's really push it: can you make the time step yet again ten times larger?

Bob: Going around a rather eccentric Kepler orbits a few times, with only a hundred steps in total? Well, we can always try.

 |gravity> ruby integrator_driver3c.rb < euler.in
 dt = 0.1
 dt_dia = 10
 dt_out = 10
 dt_end = 10
 method = yo6
 at time t = 0, after 0 steps :
   E_kin = 0.125 , E_pot =  -1 , E_tot = -0.875
              E_tot - E_init = 0
   (E_tot - E_init) / E_init =-0
 at time t = 10, after 100 steps :
   E_kin = 0.125 , E_pot =  -0.605 , E_tot = -0.481
              E_tot - E_init = 0.394
   (E_tot - E_init) / E_init =-0.451
   1.0000000000000000e+00
   1.0619008919577413e+00 -1.2659613458920589e+00
  -2.3237432724190762e-02  4.9855659376135231e-01

6.4. Spooky

Alice: All good things come to an end. We finally found the limit of your new code, but only barely: while the error is of order unity, the system hasn't really exploded numerically yet.

Bob: Let's change time step values a bit more carefully. How about something in between 0.1 and 0.01. I'll take 0.04:

 |gravity> ruby integrator_driver3d.rb < euler.in
 dt = 0.04
 dt_dia = 10
 dt_out = 10
 dt_end = 10
 method = yo6
 at time t = 0, after 0 steps :
   E_kin = 0.125 , E_pot =  -1 , E_tot = -0.875
              E_tot - E_init = 0
   (E_tot - E_init) / E_init =-0
 at time t = 10, after 250 steps :
   E_kin = 0.513 , E_pot =  -1.39 , E_tot = -0.879
              E_tot - E_init = -0.00351
   (E_tot - E_init) / E_init =0.00402
   1.0000000000000000e+00
   5.8605062658932228e-01 -4.1556477918009915e-01
   1.0033546518756853e+00  1.4169619805243588e-01

Alice: Ah, good, less than a percent error in relative total energy conservations. We're getting somewhere in our testing. Let's halve the time step. If your yo6 method is really sixth-order, halving the time step should make the result 64 times more accurate.

Bob: Here we go:

 |gravity> ruby integrator_driver3e.rb < euler.in
 dt = 0.02
 dt_dia = 10
 dt_out = 10
 dt_end = 10
 method = yo6
 at time t = 0, after 0 steps :
   E_kin = 0.125 , E_pot =  -1 , E_tot = -0.875
              E_tot - E_init = 0
   (E_tot - E_init) / E_init =-0
 at time t = 10, after 500 steps :
   E_kin = 0.554 , E_pot =  -1.43 , E_tot = -0.875
              E_tot - E_init = -1.49e-07
   (E_tot - E_init) / E_init =1.7e-07
   1.0000000000000000e+00
   5.9887919973409587e-01 -3.6203156818146032e-01
   1.0311098923820705e+00  2.1157132982705190e-01

Alice: Hmm, that's much much more improvement than a factor 64. I guess the run with a time step of 0.04 was not yet in the linear regime.

Bob: I'll halve the time step again, to 0.01:

 |gravity> ruby integrator_driver3b.rb < euler.in
 dt = 0.01
 dt_dia = 10
 dt_out = 10
 dt_end = 10
 method = yo6
 at time t = 0, after 0 steps :
   E_kin = 0.125 , E_pot =  -1 , E_tot = -0.875
              E_tot - E_init = 0
   (E_tot - E_init) / E_init =-0
 at time t = 10, after 1000 steps :
   E_kin = 0.554 , E_pot =  -1.43 , E_tot = -0.875
              E_tot - E_init = 1.23e-14
   (E_tot - E_init) / E_init =-1.41e-14
   1.0000000000000000e+00
   5.9960497793690160e-01 -3.6065834429401844e-01
   1.0308122043933747e+00  2.1385575804694398e-01

Alice: Again an improvement of far far more than a factor of 64. What is going on?

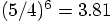Bob: This is almost spooky. The integrator has no right to converge that fast.

6.5. An Orbit Segment

Alice: The problem may be that we follow a particle through pericenter with enormously long time steps, compared with the pericenter passage time. Who knows how all the local errors accumulate and/or cancel out. It may be better to take only a small orbit segment. If we integrate for less than one time unit, we know for sure that the two bodies have not reached each other at periastron, according to what we saw before. Remember, we start our integration at apastron.

Bob: I'm happy to try that. Let us take a total integration time of 0.2, and compare a few large time step choices. Unless we make those steps pretty large, we will just get machine accuracy back, and we won't learn anything. Let's take a time step of 0.1 first:

 |gravity> ruby integrator_driver3f.rb < euler.in
 dt = 0.1
 dt_dia = 0.2
 dt_out = 0.2
 dt_end = 0.2
 method = yo6
 at time t = 0, after 0 steps :
   E_kin = 0.125 , E_pot =  -1 , E_tot = -0.875
              E_tot - E_init = 0
   (E_tot - E_init) / E_init =-0
 at time t = 0.2, after 2 steps :
   E_kin = 0.14 , E_pot =  -1.02 , E_tot = -0.875
              E_tot - E_init = 4.58e-11
   (E_tot - E_init) / E_init =-5.24e-11
   1.0000000000000000e+00
   9.7991592024615404e-01  9.9325553458239929e-02
  -2.0168916126858463e-01  4.8980438271673599e-01

And then twice as long a time step, of 0.2. Perhaps we will finally get a factor of 64 in degradation of energy conservation:

 |gravity> ruby integrator_driver3g.rb < euler.in
 dt = 0.2
 dt_dia = 0.2
 dt_out = 0.2
 dt_end = 0.2
 method = yo6
 at time t = 0, after 0 steps :
   E_kin = 0.125 , E_pot =  -1 , E_tot = -0.875
              E_tot - E_init = 0
   (E_tot - E_init) / E_init =-0
 at time t = 0.2, after 1 steps :
   E_kin = 0.14 , E_pot =  -1.02 , E_tot = -0.875
              E_tot - E_init = 2.16e-09
   (E_tot - E_init) / E_init =-2.46e-09
   1.0000000000000000e+00
   9.7991596638987577e-01  9.9325498370889442e-02
  -2.0168893933388904e-01  4.8980439348592314e-01

Alice: Much better this time. A factor of 47, in between 32 and 64. This by itself would suggest that your new method is somewhere in between fifth order and sixth order in accuracy.

Bob: And most likely sixth order: the ratio of 64/47=1.4 is smaller than the ratio of 47/32=1.5, so we are logarithmically closer to 64 than to 32.

6.6. Victory

Alice: However, we should be able to settle this more unequivocally. The problem is, we don't have much wiggle room: we don't want the total time to become so long that the particles reach pericenter, yet when we make the total integration time much shorter, we don't have room left for even a single time step -- unless we invite machine accuracy again.

Bob: Of course, we can look for a different type of orbit, but then we have to start our analysis all over again. How about this: let's take a total time of 0.5 units, while giving our particles the choice to cross this sea of time in either four or five time steps. We can start with a time step of 0.1:

 |gravity> ruby integrator_driver3h.rb < euler.in
 dt = 0.1
 dt_dia = 0.5
 dt_out = 0.5
 dt_end = 0.5
 method = yo6
 at time t = 0, after 0 steps :
   E_kin = 0.125 , E_pot =  -1 , E_tot = -0.875
              E_tot - E_init = 0
   (E_tot - E_init) / E_init =-0
 at time t = 0.5, after 5 steps :
   E_kin = 0.232 , E_pot =  -1.11 , E_tot = -0.875
              E_tot - E_init = 9.08e-10
   (E_tot - E_init) / E_init =-1.04e-09
   1.0000000000000000e+00
   8.7155094516550113e-01  2.3875959971050609e-01
  -5.2842606676242798e-01  4.2892868844542126e-01

And then repeat the procedure for a time step of 0.125.

Alice: Ah, before you start the run, let's make a prediction: the energy conservation degradation should be .

 |gravity> ruby integrator_driver3i.rb < euler.in
 dt = 0.125
 dt_dia = 0.5
 dt_out = 0.5
 dt_end = 0.5
 method = yo6
 at time t = 0, after 0 steps :
   E_kin = 0.125 , E_pot =  -1 , E_tot = -0.875
              E_tot - E_init = 0
   (E_tot - E_init) / E_init =-0
 at time t = 0.5, after 4 steps :
   E_kin = 0.232 , E_pot =  -1.11 , E_tot = -0.875
              E_tot - E_init = 3.35e-09
   (E_tot - E_init) / E_init =-3.83e-09
   1.0000000000000000e+00
   8.7155095947304040e-01  2.3875959630280436e-01
  -5.2842603945420896e-01  4.2892869095118885e-01

Bob: And by dividing the total energy errors of the last two runs we get a ratio of 3.69.

Alice: Not bad at all! Just three percent short of what we had expected for a sixth-order integration scheme. I think we can now officially declare your yo6 to be worthy of the 6 in it's name!

But I must say, I'm still deeply puzzled and surprised that seven leapfrog calls, involving four rather funny numbers, can suddenly emulate a Runge-Kutta.

Bob: According to my source, it is more than `emulate': this particular combination of leapfrog calls is nothing else but a Runge-Kutta scheme.