9. A Four-Step Method
Bob: Ready to go for a fourth-order multi-step algorithm?
Alice: Ready whenever you are!
Bob: I'll start by repeating the steps I showed you for the second-order
algorithm. Instead of Eq. (53), we now have to expand
the acceleration in a Taylor series up to the crackle:
Bob: Just a little. Good luck!
Alice: Oh, I have to do it again? Well, I guess I sort-of like doing
this, up to a point.
Bob: And if you dislike it, you certainly dislike it far less than I do.
Alice: Okay, I'll do it. From Eq. (73) we can form the following
linear combination, subtracting the second equation from twice the
first one, in order to eliminate the term with the jerk in it. Similarly,
we can subtract the third equation from thrice the first one, and we wind
up with two equations for the two remaining variables, the snap
Alice: Each next one will only get easier. I'll substitute Eq. (75)
in the top line of Eq. (74), and that should do it:
Bob: Not if you do it, no. Keep up the good work!
Alice: Now for the home run. I'll substitute Eqs. (75) and (77)
in the top line of Eq. (73), and get:
Bob: If you didn't make a mistake anywhere, that is.
Alice: I thought it was your job to check whether I was not making any
mistake!
Bob: I think you didn't make any. But as you so often say, it doesn't
hurt to check.
Alice: I can't very well argue with myself, can I? Okay, how shall we
check things. Doing the same things twice is not the best way to test my
calculations, since I may well make the same mistake the second time, too.
It would be much better to come up with an independent check. Ah, I
see what we can do: in Eq. (73), I can check whether the solutions
I just obtained for for
Here is the first one:
Bob: We were trying to get an expression for the acceleration at time
zero, to third order in the time step, expressed in terms of the previous
three accelerations. So all we have to do is to plug your results back
into Eq. (72).
Alice: Ah, yes, it's easy to forget the thread of a story, if you get lost
in eliminations.
Bob: So now it's my turn, I guess. Let me code up your results. I'll open
a new file, ms4body.rb. Let me first have a look at the
previous second-order method ms2, for comparison:
Our fourth-order multi-step method should be called ms4,
clearly. I'll use rk4 to rev up the engine, something we'll
have to do three times now. And instead of using snap and crackle
out-of-the-box, so to speak, I'll use them with the appropriate factors
of the time step,
Here are the equations that we have to code up, as a generalization of
Eq. (57):
Alice: That's not so much longer than ms2, and it still looks
neat and orderly! And wait, you have used the division method for our
Vector class, in dividing by those number like
Bob: That's true! I hadn't even thought about it; it was so natural
to do that. What did you say again, when I told you I had added division,
together with subtraction, to the Vector class?
Alice: I said that I was sure it would come in handy sooner or later.
Bob: I guess it was sooner rather than later.
Alice: And I see that you have abbreviated the names of the variables
somewhat. Instead of @prev_acc for the previous acceleration,
you now use @ap1, for the first previous acceleration, I guess.
And then, for the yet more previous acceleration before that, you use
@ap2, and so on.
Bob: Yes. I would have like to write a-2 for
Alice: Time to test ms4.
Bob: Yes, and we may as well start again with the
same values as we have been using recently:
Alice: Now that everything works, how about trying to apply a
corrector loop? In the case of your second-order version, we saw
that there was no need to bother doing so, since we convinced ourselves
that we just got the leapfrog method back. But that must have been a
low-order accident. The fourth-order predictor-corrector version will
surely lead to a new algorithm, one that you haven't already implemented
in our N-body code.
Bob: I bet you're right. Okay, let's do it!
Alice: Given that I already reconstructed your instructions on paper before,
I only have to extend it to two orders higher. Here are the results
on a backward extrapolation, starting with the predicted values at time
The same arguments as I gave before will now lead to the following expression
for the first-iteration solution for the corrected quantities, as an extension
of Eq. (68)
Bob: And this time I certainly do not recognize these equations. It
seems that we really have a new algorithm here.
Alice: Let me see whether I can extend your code, to implement this scheme.
It would be nice to keep the number of acceleration calculations the same
as we had before, doing it only once per time step. After all, when
we will generalize this to a true N-body system, it is the calculation
of the acceleration that will be most expensive, given that for each particle
we will have to loop over all other particles.
However, I need to compute the acceleration at the end of the calculation,
at the newly predicted position. This means that I then have to remember
the value of the acceleration, so that I could reuse it at the
beginning of the next time step. This means that I will have to change
the variable ap0 to a true instance variable @ap0, so
that it will still be there, the next time we enter ms4pc.
I will have to initialize @ap0 during the last time we use the
rk4 method, so that it is ready to be used when we finally
enter the main body of the ms4pc method, as I will call it,
to distinguish it from your previous implementation ms4.
Bob: The pc stands for predictor-corrector version, I take it.
Alice: Indeed. Well, the rest is just a matter of coding up the
equations we just wrote out. Of course, in the predictor step,
there is no need to compute the predicted velocity. It is only the
predicted position that we need in order to obtain the acceleration
at the new time, and through that, the jerk.
What do you think of this:
Bob: That ought to work, with a little bit of luck, if we didn't
overlook any typos or logopos.
Alice: Logopos?
Bob: Errors in logic, as opposed to typing.
Alice: Yes, both are equally likely to have slipped in.
Let's try to run it and if it runs,
let's see how well we're doing:
Bob: And it is . . . . a logopo!
Alice: And an inscrutable logopo to boot: what does that mean,
undefined method `-@' ?!? Just when I grew fond of Ruby,
it gives us that kind of message -- just to keep us on our toes,
I guess.
Bob: Beats me. I know what the method - is, that is just
the subtraction method, which I have neatly defined for our Vector
class, while I was implementing the second-order version of our series
of multi-step integrators. I have no idea as to what the method
-@ could possibly be.
But let us look at the code first, maybe that will tell us something.
I'll scrutinize all the minus signs, to see whether we can find a clue
there. The middle part of the method ms4pc is the same as in
the predictor-only method ms4, and that one did not give any
errors. So we'll have to look in the last five lines. The first three
of those are verbatim copies of the lines above, which were already tested,
we the culprit really should lurk somewhere in the last two lines.
Hmm, minus sign, last two lines, ahaha! Unary minus!!
Alice: Unary minus?? As opposed to a dualistic minus?
Bob: As opposed to a binary minus. There are two different meanings
of a minus sign, logically speaking: the minus in
So in the first case, you have a binary operator, with two arguments,
and in the second case, you have a unary operator, with only one argument.
Hence the name `unary minus.'
Alice: A binary minus, hey? I'm getting more and more confused with all
those different things that are called binaries. In astronomy we call
double stars binaries, in computer science they use binary trees in data
structures, and binary notation for the ones and zeros in a register,
and we talk about binary data as opposed to ASCII data, and now even a
lowly minus can become a binary. Oh well, I guess each use has its own
logic.
Bob: And many things in the universe come in pairs.
Alice: Even people trying to write a toy model and stumbling upon unary
minuses -- or unary mini? Anyway, I see now that the minus sign that I
added in front of the jerk in the middle of the line
was a unary minus. All very logical. And yes, while we had defined a
binary minus before, we had not yet defined a unary minus.
Bob: So you committed a logopo.
Alice: And I could correct my logopo by writing jdt/(-2.0)
instead of -jdt/2.0. However, I don't like to do that, it looks
quite ugly.
Bob: The alternative is to add a unary minus to our Vector class.
Alice: I would like that much better! How do you do that?
Bob: Judging from the error message, Ruby seems to use the convention
that -@ stands for unary minus. But just to make sure, let me
look at the manual. Just a moment . . .
. . . and yes, my interpretation was correct. So let's just add it to
our collections of methods in the file vector.rb. How about
the following extension, within the Vector class:
and for good measure, I may as well add a unary plus too:
Alice: I see, just in case you write something like r_new = +r_old.
Bob: Exactly. No need to do so, but also no need to let that give you
an error message if you do.
9.1. Combinatorics
, 
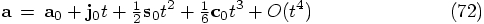
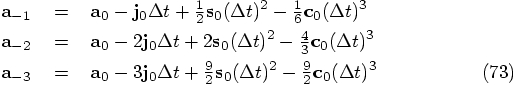
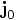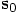and 
,
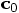which we can then use in Eq. (72). The only difference is
that the inversion is a little harder than it was for getting
Eq. (55).
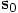and the crackle 
:
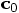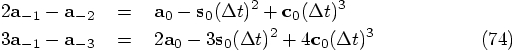
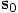, in order to obtain
an equation for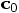 
, as follows:
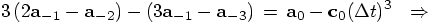
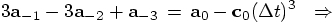
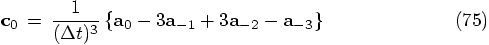
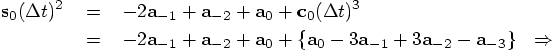
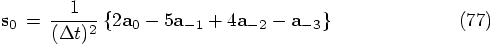
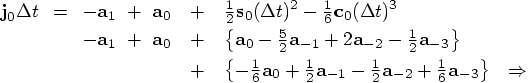
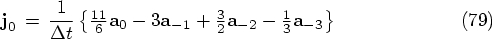
9.2. Checking
, 
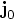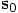and
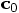indeed give us those previous three accelerations back
again. In each of those three cases, I'll start off with the right-hand
sides of the equation, to see whether I'll get the left-hand side back.
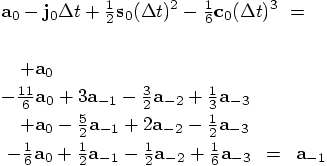
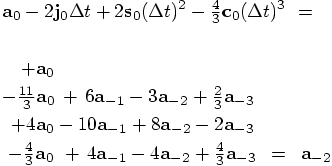
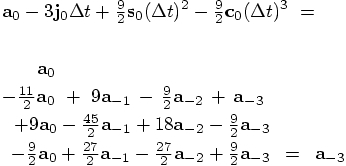
9.3. Implementation
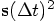and
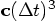, respectively.
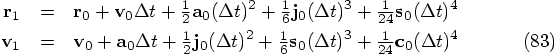
and
so on.
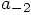but that would be interpreted as a subtraction of the number
2 from the variable a, so I choose @ap2, for
a-previous-two.
9.4. Testing
|gravity> ruby integrator_driver4d.rb < euler.in
dt = 0.01
dt_dia = 0.1
dt_out = 0.1
dt_end = 0.1
method = ms4
at time t = 0, after 0 steps :
E_kin = 0.125 , E_pot = -1 , E_tot = -0.875
E_tot - E_init = 0
(E_tot - E_init) / E_init =-0
at time t = 0.1, after 10 steps :
E_kin = 0.129 , E_pot = -1 , E_tot = -0.875
E_tot - E_init = 1.29e-10
(E_tot - E_init) / E_init =-1.48e-10
1.0000000000000000e+00
9.9499478015881193e-01 4.9916426246428156e-02
-1.0020902652762116e-01 4.9748796059474770e-01
A good start. Now for time steps that are ten times smaller:
|gravity> ruby integrator_driver4e.rb < euler.in
dt = 0.001
dt_dia = 0.1
dt_out = 0.1
dt_end = 0.1
method = ms4
at time t = 0, after 0 steps :
E_kin = 0.125 , E_pot = -1 , E_tot = -0.875
E_tot - E_init = 0
(E_tot - E_init) / E_init =-0
at time t = 0.1, after 100 steps :
E_kin = 0.129 , E_pot = -1 , E_tot = -0.875
E_tot - E_init = 2.24e-14
(E_tot - E_init) / E_init =-2.56e-14
1.0000000000000000e+00
9.9499478008957187e-01 4.9916426216151437e-02
-1.0020902860087451e-01 4.9748796006061335e-01
Alice: Congratulations! But this is close to machine accuracy.
Can you just double the time step, to check whether the errors get
16 times larger?
|gravity> ruby integrator_driver4f.rb < euler.in
dt = 0.002
dt_dia = 0.1
dt_out = 0.1
dt_end = 0.1
method = ms4
at time t = 0, after 0 steps :
E_kin = 0.125 , E_pot = -1 , E_tot = -0.875
E_tot - E_init = 0
(E_tot - E_init) / E_init =-0
at time t = 0.1, after 50 steps :
E_kin = 0.129 , E_pot = -1 , E_tot = -0.875
E_tot - E_init = 3.45e-13
(E_tot - E_init) / E_init =-3.95e-13
1.0000000000000000e+00
9.9499478008976872e-01 4.9916426216220194e-02
-1.0020902859668304e-01 4.9748796006170143e-01
Bob: There you are! We indeed have a fourth-order multi-step integrator!
9.5. A Predictor-Corrector Version
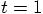, and going back to time 
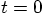, as a higher-order
analogy of Eq. (60) :
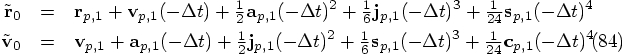
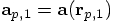and where
, 
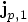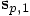, and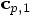 
are the jerk, snap, and crackle as determined from the values of the last
four accelerations, which are now
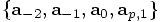, instead of
the previous series of four that were used in the prediction step, which were
.
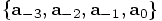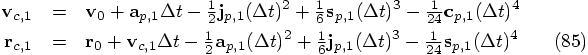
9.6. Implementation
|gravity> ruby integrator_driver4dpc_old.rb < euler.in
dt = 0.01
dt_dia = 0.1
dt_out = 0.1
dt_end = 0.1
method = ms4pc
at time t = 0, after 0 steps :
E_kin = 0.125 , E_pot = -1 , E_tot = -0.875
E_tot - E_init = 0
(E_tot - E_init) / E_init =-0
./ms4body_old.rb:158:in `ms4pc': undefined method `-@' for [-0.000500866850078996, -0.00502304344952675]:Vector (NoMethodError)
from ./ms4body_old.rb:22:in `send'
from ./ms4body_old.rb:22:in `evolve'
from integrator_driver4dpc_old.rb:21
9.7. A Logopo
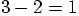and the minus in 
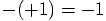. In the first example, the minus
indicates that you are subtracting two numbers. You could write
that operation as 
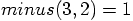. In the second example,
you are dealing only with one number, and you take the negative value
of that number. You could write that as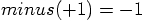 
.
@vel = old_vel + @ap0*dt + (-jdt/2.0 + sdt2/6.0 - cdt3/24.0)*dt
def -@
self.map{|x| -x}.to_v
end