



Next: 5.7 The End of
Up: 5. Exploring with a
Previous: 5.5 Priming the Pump
|gravity> leapfrog2a > leapfrog2a_0.0001_100.out
Please provide a value for the time step
0.0001
and for the duration of the run
100
Initial total energy E_in = -0.866025
Final total energy E_out = -0.866025
absolute energy error: E_out - E_in = 2.55083e-08
relative energy error: (E_out - E_in) / E_in = -4.10015e-08
|gravity>
Figure 5.10:
The fourth attempt to integrate the orbits of three stars
starting off on a circle with an initial velocity perturbation of
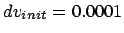 , time step
, time step 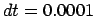 and a total duration of
and a total duration of
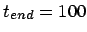
 |
- Bob:
- Still quite different pictures. And notice that the energy errors
don't yet scale with a factor of one hundred, as they would once we
really converge to a unique set of tracks -- if there is such a thing.
- Alice:
- Still doubting my suggestion, aren't you? I must admit, it doesn't
look very good, so far. But hope springs eternal, so let's try
another order of magnitude step size refinement, down to dt =
0.000,01 which implies ten million integration steps in total for
this three-body problem.
|gravity> leapfrog2a > leapfrog2a_0.00001_100.out
Please provide a value for the time step
0.00001
and for the duration of the run
100
Initial total energy E_in = -0.866025
Final total energy E_out = -0.866025
absolute energy error: E_out - E_in = -1.59043e-11
relative energy error: (E_out - E_in) / E_in = 1.83647e-11
|gravity>
Figure 5.11:
The fifth attempt to integrate the orbits of three stars
starting off on a circle with an initial velocity perturbation of
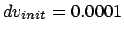 , time step
, time step 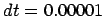 and a total duration of
and a total duration of
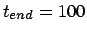
 |
- Bob:
- Surprise! Virtually the same picture, all of a sudden! So now I
agree that Alice was really right on both counts. But I have one last
worry. Why has the energy error suddenly shrunk so much, by a factor
of more than a thousand, where I would have expected only a hundred?
- Alice:
- Hard to say. In the two-body case it was not so hard to track down
all aspects of the integration errors, since the underlying orbits
were so simple. But look here, what a mess! In order to answer
your last worry, we need to build a lot more tools. Besides a switch
to variable time steps in the integrator, which we'll get around to at
some point, we need much better ways to dissect orbit segments, in
order to focus on particularly interesting interactions. Ideally, we
would like to build in some form of artificial intelligence, so that
the particles themselves will know how to take notes while they are
flying around and being flung around. When we can harvest their
stories at the end of an integration, we will have a head start in
answering questions of the type you asked. You'll have to be a bit
patient though, since it will require quite a number of sessions to
get to that point.
- Carol:
- Well, I'm game. It's a lot of fun already, to see how much progress
we have made. The fact that we have now reached a point where we can
ask questions that call for some form of artificial intelligence to
answer them is impressive enough. Besides, it means that I, too,
might start to write a working paper about part of what we are doing
now. One footnote, though: I wouldn't call these orbits a mess; on
the contrary, I find all this wheeling around quite elegant.
- Bob:
- Elegance is in the eye of the beholder, I guess, but I must admit that
I, too, find this figure skating quite pretty. And I am desperately
thinking how I could make a working paper out of all this -- perhaps
for an art class?
- Alice:
- When I called the orbits a mess, I meant it in an affectionate way.
It reminded me of my room, which I haven't cleaned up for a while, but
that's another story. How about inviting more art, and running this
thing for a hundred million time steps, by going to t_end = 1000?
- Bob:
- You have my blessing.
|gravity> leapfrog2a > leapfrog2a_0.00001_1000.out
Please provide a value for the time step
0.00001
and for the duration of the run
1000
Initial total energy E_in = -0.866025
Final total energy E_out = -0.866025
absolute energy error: E_out - E_in = -5.78748e-10
relative energy error: (E_out - E_in) / E_in = 6.6828e-10
|gravity>




Next: 5.7 The End of
Up: 5. Exploring with a
Previous: 5.5 Priming the Pump
Jun Makino
�$BJ?@.�(B18�$BG/�(B10�$B7n�(B10�$BF|�(B


