



Next: 10.2 Making gnuplot movies
Up: 10. A 25-body Example
Previous: 10. A 25-body Example
- Bob:
- Time to start a real experiment! This will be our first chance to put
our nbody_sh1.C engine to good use. I remember that we had a
number of options built in, but for simplicity, let us just use the
default settings.
- Carol:
- Fine. Let's see. that means letting the system run for 10 time units,
with energy diagnostics being output every time unit, and all that
with a standard step size control parameter of 0.03.
|gravity> sphere -n 25 | ../chap8/nbody_sh1 > s25.out
seed = 1063318557
Starting a Hermite integration for a 25-body system,
from time t = 0 with time step control parameter dt_param = 0.03 until time 10 ,
with diagnostics output interval dt_dia = 1,
and snapshot output interval dt_out = 1.
at time t = 0 , after 0 steps :
E_kin = 0 , E_pot = -0.571622 , E_tot = -0.571622
absolute energy error: E_tot - E_init = 0
relative energy error: (E_tot - E_init) / E_init = -0
at time t = 1.00026 , after 4154 steps :
E_kin = 1.57024 , E_pot = -2.14216 , E_tot = -0.571911
absolute energy error: E_tot - E_init = -0.000289307
relative energy error: (E_tot - E_init) / E_init = 0.000506117
at time t = 2.00002 , after 15063 steps :
E_kin = 0.574657 , E_pot = -1.14657 , E_tot = -0.571912
absolute energy error: E_tot - E_init = -0.000289794
relative energy error: (E_tot - E_init) / E_init = 0.000506968
at time t = 3.00001 , after 24785 steps :
E_kin = 0.735507 , E_pot = -1.30742 , E_tot = -0.571913
absolute energy error: E_tot - E_init = -0.000290734
relative energy error: (E_tot - E_init) / E_init = 0.000508612
at time t = 4.00002 , after 37188 steps :
E_kin = 1.1189 , E_pot = -1.69081 , E_tot = -0.571914
absolute energy error: E_tot - E_init = -0.000291627
relative energy error: (E_tot - E_init) / E_init = 0.000510175
at time t = 5.00002 , after 60274 steps :
E_kin = 1.07524 , E_pot = -1.64716 , E_tot = -0.571917
absolute energy error: E_tot - E_init = -0.000294566
relative energy error: (E_tot - E_init) / E_init = 0.000515317
at time t = 6 , after 109752 steps :
E_kin = 1.68677 , E_pot = -2.25869 , E_tot = -0.571926
absolute energy error: E_tot - E_init = -0.000304007
relative energy error: (E_tot - E_init) / E_init = 0.000531832
at time t = 7 , after 445974 steps :
E_kin = 1.9559 , E_pot = -2.52792 , E_tot = -0.572019
absolute energy error: E_tot - E_init = -0.000396555
relative energy error: (E_tot - E_init) / E_init = 0.000693737
at time t = 8 , after 805101 steps :
E_kin = 0.579634 , E_pot = -1.15175 , E_tot = -0.572118
absolute energy error: E_tot - E_init = -0.000495676
relative energy error: (E_tot - E_init) / E_init = 0.000867139
at time t = 9 , after 1164240 steps :
E_kin = 1.51451 , E_pot = -2.08673 , E_tot = -0.572217
absolute energy error: E_tot - E_init = -0.000595069
relative energy error: (E_tot - E_init) / E_init = 0.00104102
at time t = 10 , after 1523388 steps :
E_kin = 2.16613 , E_pot = -2.73845 , E_tot = -0.572317
absolute energy error: E_tot - E_init = -0.000694481
relative energy error: (E_tot - E_init) / E_init = 0.00121493
|gravity>
- Alice:
- This is fun. We are now really moving a bunch of stars around!
- Carol:
- But the energy conservation is not great: at the end the accumulated
energy error has reached more than 0.1% of the initial energy value.
- Bob:
- Also, something funny happened around
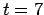 : until then each time unit
of integration required at most a few tens of thousands of steps, but
suddenly between
: until then each time unit
of integration required at most a few tens of thousands of steps, but
suddenly between 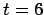 and
and 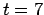 a few hundred thousand steps were needed.
And each subsequent time unit turned out to be equally computationally
expensive.
a few hundred thousand steps were needed.
And each subsequent time unit turned out to be equally computationally
expensive.
- Carol:
- Let us first address the question of energy conservation, by doing a
new run with a three times smaller accuracy parameter. To cut down a
bit on output, let us report energy changes only once every two time units,
as follows.
|gravity> sphere -n 25 | ../chap8/nbody_sh1 -d 0.01 -e 2 > s25a.out
seed = 1063319094
Starting a Hermite integration for a 25-body system,
from time t = 0 with time step control parameter dt_param = 0.01 until time 10 ,
with diagnostics output interval dt_dia = 2,
and snapshot output interval dt_out = 1.
at time t = 0 , after 0 steps :
E_kin = 0 , E_pot = -0.603695 , E_tot = -0.603695
absolute energy error: E_tot - E_init = 0
relative energy error: (E_tot - E_init) / E_init = -0
at time t = 2.00003 , after 30794 steps :
E_kin = 0.603447 , E_pot = -1.20714 , E_tot = -0.603695
absolute energy error: E_tot - E_init = -9.9949e-09
relative energy error: (E_tot - E_init) / E_init = 1.65562e-08
at time t = 4.00005 , after 56055 steps :
E_kin = 0.711514 , E_pot = -1.31521 , E_tot = -0.603695
absolute energy error: E_tot - E_init = -1.09129e-08
relative energy error: (E_tot - E_init) / E_init = 1.80768e-08
at time t = 6.00024 , after 91101 steps :
E_kin = 0.309542 , E_pot = -0.913237 , E_tot = -0.603695
absolute energy error: E_tot - E_init = -1.33915e-08
relative energy error: (E_tot - E_init) / E_init = 2.21825e-08
at time t = 8.00012 , after 117285 steps :
E_kin = 0.584493 , E_pot = -1.18819 , E_tot = -0.603695
absolute energy error: E_tot - E_init = -1.38143e-08
relative energy error: (E_tot - E_init) / E_init = 2.28829e-08
at time t = 10 , after 146608 steps :
E_kin = 0.905758 , E_pot = -1.50945 , E_tot = -0.603695
absolute energy error: E_tot - E_init = -1.48435e-08
relative energy error: (E_tot - E_init) / E_init = 2.45878e-08
|gravity>
- Bob:
- How curious! Indeed, the energy error is far smaller now, as we had
hoped, but the total number of steps needed has been cut dramatically,
by more than a factor ten, from more than one and a half million to
less than hundred-fifty thousand. All this while we would naively have
expected an increase by a factor three! What is going on?
- Alice:
- We have started with a different random number seed. Perhaps there
are large fluctuations from run to run in the difficulty of the
integration? Let us do a few more runs, to compare. Since we are
mostly interested in the bottom line, let us give output only at the
end of the run, while throwing away the actual snapshot outputs.
|gravity> sphere -n 25 | ../chap8/nbody_sh1 -d 0.01 -e 10 > /dev/null
seed = 1063319209
Starting a Hermite integration for a 25-body system,
from time t = 0 with time step control parameter dt_param = 0.01 until time 10 ,
with diagnostics output interval dt_dia = 10,
and snapshot output interval dt_out = 1.
at time t = 0 , after 0 steps :
E_kin = 0 , E_pot = -0.527251 , E_tot = -0.527251
absolute energy error: E_tot - E_init = 0
relative energy error: (E_tot - E_init) / E_init = -0
at time t = 10 , after 802102 steps :
E_kin = 0.665259 , E_pot = -1.19251 , E_tot = -0.527251
absolute energy error: E_tot - E_init = -1.22308e-07
relative energy error: (E_tot - E_init) / E_init = 2.31974e-07
|gravity> !!
sphere -n 25 | ../chap8/nbody_sh1 -d 0.01 -e 10 > /dev/null
seed = 1063319458
Starting a Hermite integration for a 25-body system,
from time t = 0 with time step control parameter dt_param = 0.01 until time 10 ,
with diagnostics output interval dt_dia = 10,
and snapshot output interval dt_out = 1.
at time t = 0 , after 0 steps :
E_kin = 0 , E_pot = -0.557163 , E_tot = -0.557163
absolute energy error: E_tot - E_init = 0
relative energy error: (E_tot - E_init) / E_init = -0
at time t = 10 , after 1140982 steps :
E_kin = 0.723355 , E_pot = -1.28052 , E_tot = -0.557164
absolute energy error: E_tot - E_init = -5.67934e-07
relative energy error: (E_tot - E_init) / E_init = 1.01933e-06
|gravity>
- Carol:
- You are right about the fluctuations, the run-to-run differences are huge.
- Alice:
- Let us see whether we can reason our way to an answer. We are using
an integrator that determines its step size automatically, depending on
how close individual stars approach each other. This means that the
expensive runs that take so long must contain situations where stars
are very close together for very long times.
- Bob:
- How can stars stay together so long? They don't stick together, do
they? We are using point particles with zero diameter, so they can't
collide.
- Alice:
- Two stars don't stay together for long when they pass by each other
occasionally. The only explanation I can think of is that two or more
stars are captured in very tight bound systems, a situation that would
force the shared time step to become very small, slowing down all
other stars as well.
- Bob:
- Ah, and as long as those stars stay together, the computation remains
very expensive. And a very close double star must be stable, as long
as no other star comes close enough to disrupt it.
- Alice:
- And the smaller the double star is, the smaller a target it forms, and
the less likely it is that it will be disrupted. At the same time, by
being smaller such a double star forces the whole system on its knees,
by pushing the shared time step to a very small value. These two
properties conspire to produce large fluctuations!
- Carol:
- An interesting hypothesis, but is it true? Clearly, we have to
investigate this. By now I don't want to rely on plausibility any
more, given how we almost made a big mistaken.
- Alice:
- I would like to to make sure too. Now we have to find a way to check
whether whether our system forms double stars - or binaries, as we
astronomers tend to call them.
- Bob:
- That reminds me of the binars, from Startrek; I guess they formed a
type of double star too. But seriously, how about just making a
movie, and see whether stars are pairing up. Can you do that with
gnuplot?
- Carol:
- I believe so. But we'll have to do some awk work to make it work.
- Bob:
- Sounds pretty awkward to me, since I don't know anything about awk.
- Carol:
- Yeah, it takes a while to get the hang of it. But it's a good
investment of time, for sure: once you know your way around with
awk, you can quickly manipulate all find of data without the
need to write ponderous programs in C++ or similar languages.
While awk is not a very fast language, in many cases we don't
particularly care about speed, if it is just a matter of a few
straightforward conversions.
- Alice:
- Do I hear you volunteering for writing the scripts to let us allow to
watch movies of our
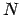 -body run?
-body run?
- Carol:
- Okay, I'll do so. In fact, I have to do an awk project anyway,
as homework for a class, so this will be it.




Next: 10.2 Making gnuplot movies
Up: 10. A 25-body Example
Previous: 10. A 25-body Example
Jun Makino
�$BJ?@.�(B18�$BG/�(B10�$B7n�(B10�$BF|�(B