10.3 Performing an experiment

Carol:

I don't vouch for anything, but let's see what comes up.

|gravity> makemovie1.csh nbody1.out
rm: No match.
2 nbody1.out
snapno = 1
snapno = 2
snapno = 3
snapno = 4
snapno = 5
snapno = 6
snapno = 7
snapno = 8
snapno = 9
snapno = 10
Hit return to exit
|gravity>

Figure 10.1: 1st frame of the first movie

Figure 10.2: 2nd frame of the first movie

Figure 10.3: 3rd frame of the first movie

Figure 10.4: 4th frame of the first movie

Figure 10.5: 5th frame of the first movie

Figure 10.6: 6th frame of the first movie

Figure 10.7: 7th frame of the first movie

Figure 10.8: 8th frame of the first movie

Figure 10.9: 9th frame of the first movie

Figure 10.10: 10th frame of the first movie

Carol:

I guess I passed, yes? You want my autograph?

Alice:

Did you see individual stars escaping? Real astrophysics going on here, lady and gentleman!

Bob:

Yes, I saw some stars boiling off into deep space, but I must admit, I couldn't quite follow what was happening in the inner core. It was worse than the old slapstick: everything was moving just too fast.

Carol:

Lets get ten times as many snapshot frames, but decreasing the output time intervals from the default of one time unit to one tenth of a time unit.

Bob:

Let's see, right, that was option -o 0.1, with o standing for output interval. If I work with this code a few more times I'll get familiar with all the options. Let's see what happens now.

|gravity> ../chap9/sphere -n 25 | ../chap8/nbody_sh1 -o 0.1 -e 10 > nbody2.out
seed = 1064697607
Starting a Hermite integration for a 25-body system,
  from time t = 0 with time step control parameter dt_param = 0.03  until time 10 ,
  with diagnostics output interval dt_dia = 10,
  and snapshot output interval dt_out = 0.1.
at time t = 0 , after 0 steps :
  E_kin = 0 , E_pot = -0.53095 , E_tot = -0.53095
                absolute energy error: E_tot - E_init = 0
                relative energy error: (E_tot - E_init) / E_init = -0
at time t = 10 , after 102258 steps :
  E_kin = 0.523367 , E_pot = -1.05432 , E_tot = -0.530958
                absolute energy error: E_tot - E_init = -8.39424e-06
                relative energy error: (E_tot - E_init) / E_init = 1.58099e-05
|gravity>

Carol:

Again, a reasonable relative energy, comparable to what we had before. Now let us follow all those stars step by step.

|gravity> makemovie1.csh nbody2.out
rm: No match.
2 nbody2.out
snapno = 1
snapno = 2
snapno = 3
 . . . .
snapno = 98
snapno = 99
snapno = 100
Hit return to exit
|gravity>

Figure 10.11: Last frame of the second movie, from the data stored in nbody2.out

Bob:

That's more like it. Now we can really follow what's going on.

Carol:

Well, yes and no. We can now follow the individual particles all right, but what about those binaries that Alice had promised us, as the explanation for the mysterious increase in computer time that we saw yesterday?

Alice:

Well, I'm not sure. But my guess would be that those binaries are too small to see easily, on the scale we have plotted them. After all, they were so compute expensive exactly because the two stars of such a binary were bound in a short orbit - or so we hypothesized.

Bob:

Even so, wouldn't we have clearly seen that there were places where two symbols on the screen almost overlapped?

Carol:

I do believe I saw a few cases like that, but I can't be completely sure.

Alice:

The other problem is that binaries are more massive than single stars, so they tend to sink to the center of a star cluster, where everything is more crowded. This is due to equipartition.

Bob:

And what is equipartition?

Alice:

It is an effect that is similar to what happens with molecules in the air. Carbon dioxide molecules, for example, are heavier than other molecules in air, and therefore they tend to stay lower.

Carol:

Yes, I remember my high school teacher taking a beaker with carbon dioxide, which he had obtained from a pressure cylinder. And then he poured the invisible gas over a flame, dousing it immediately. It was very impressive.

Bob:

But how come that carbon dioxide does not fall out of the air? I thought it was mixed rather thoroughly in the air around us.

Alice:

That's because air currents tend to mix all gases, light or heavy. Even grass pollen, which are far more heavier than any gas molecule are carried along with the slightest breeze.

Carol:

Tell me all about it. My allergy season is about to come up again, which is no fun.

Alice:

However, when you carefully pour carbon dioxide, it will stay at the bottom of a room for a while. Similarly, a lighter gas, like helium, will flow up - which is the reason that a helium balloon indeed rises, even though the plastic surrounding the helium is heavier than air.

Bob:

But what does all that have to do with binaries sinking to the center of a star cluster?

Alice:

The combined gravitational force of all the stars points toward the center of the cluster. Heavier `molecules', in our case binaries, therefore tend to sink to the center, just like carbon dioxide molecules tend to sink to the floor of a lab.

Carol:

All nice and fine, but we're now speculating on and on about binaries, and we're not yet sure whether we've seen one. Aren't we running the danger of discussing how many angles can dance on the tip of a needle?

Bob:

In order to dance together, perhaps angles have to form binaries too?

Carol:

You're now imagining binaries everywhere. I want proof.

Alice:

I have an idea. Rather than trying to peer in more and more details at those movie frames, why not build a binary detector!

Bob:

A binary detector?

Alice:

Yes! Just like physicists build elementary particle detectors, which they use in their accelerators to see what they've got, after smashing subatomic particles into each other.

Bob:

That makes sense. After all, we have build a star accelerator, in the form of our $N$-body integrator nbody_sh1.C. Our movie was in fact a star detector. So it would be a logical next step to build a more sophisticated and specialized detector, one that would only be triggered by binaries.

Carol:

That sounds like fun. But how to go about it?

Alice:

The idea is simple. You just check all possible pairs of particles, and check to see which ones are bound together, forming a binary.

Carol:

That's reasonable, since even with 25 particles, and 100 snapshots, you only have to check 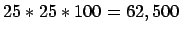$25*25*100 = 62,500$ pairs, and with so many millions of floating point operations per second, even on laptops, that should be no problem.

Bob:

After all, at every time step we had to compute the pairwise forces, which meant 625 pairwise forces far much more often than 100 times in our run. So time won't be a problem. But what type of algorithm would you use?

Alice:

I'm afraid we would have to start with a reasonable amount of celestial mechanics. And rather than trying to derive all the relationships from scratch, let's get together again tomorrow. I'll bring my celestial mechanics book with me, and then we can figure it out.