6.6 The Hermite Soars: Three Bodies on a Figure Eight

Bob:

Here is the code. Rather than doing another diff, since this is a new problem I will list it in full.

Bob:

And here are the results. Another fifth-order error behavior!

|gravity> g++ -o hermite2 hermite2.C
|gravity> hermite2 > hermite2_0.01_100.out
Please provide a value for the time step
0.01
and for the duration of the run
100
Initial total energy E_in = -1.28705
Final total energy E_out = -1.28705
absolute energy error: E_out - E_in = -3.81996e-07
relative energy error: (E_out - E_in) / E_in = 2.96801e-07
|gravity>

|gravity> hermite2 > hermite2_0.001_100.out
Please provide a value for the time step
0.001
and for the duration of the run
100
Initial total energy E_in = -1.28705
Final total energy E_out = -1.28705
absolute energy error: E_out - E_in = -4.00457e-12
relative energy error: (E_out - E_in) / E_in = 3.11144e-12
|gravity>

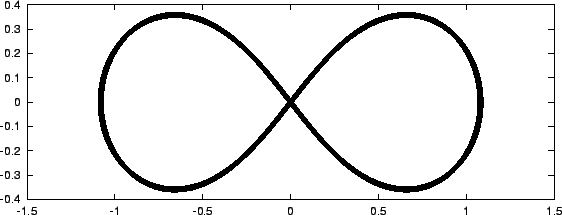
Figure 6.4: The second Hermite attempt to integrate the orbits of three stars starting off on a figure-8 orbit with an initial velocity perturbation of 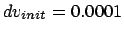$dv_{init}=0.0001$, time step 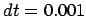$dt = 0.001$ and a total duration of $t_{end} = 100$

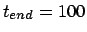
Alice:

Well, all I can say is that the regularity of the orbit probably gives rise to cancellations. This is a well-known phenomenon for the leapfrog, for example, where sometimes the errors accumulate in the phases more than the energies of the particles. I suggest to come back to this question by the time we try our hand at larger 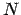$N$-body calculations starting from more random, less regular initial conditions.

Bob:

Okay! And here are the timings Carol asked for:

|gravity> time leapfrog3a > /dev/null
Please provide a value for the time step
0.00001
and for the duration of the run
100
Initial total energy E_in = -1.287
Final total energy E_out = -1.287
absolute energy error: E_out - E_in = -1.24349e-11
relative energy error: (E_out - E_in) / E_in = 9.66196e-12
19.520u 0.100s 0:24.34 80.6%	0+0k 0+0io 168pf+0w
|gravity> time hermite2 > /dev/null
Please provide a value for the time step
0.001
and for the duration of the run
100
Initial total energy E_in = -1.28705
Final total energy E_out = -1.28705
absolute energy error: E_out - E_in = -4.00457e-12
relative energy error: (E_out - E_in) / E_in = 3.11144e-12
0.790u 0.010s 0:05.75 13.9%	0+0k 0+0io 169pf+0w
|gravity>

Carol:

Not bad! The Hermite is more accurate, even for time steps that are a hundred times larger. Of course, each time step is more complicated than the leapfrog, so the time gain is less than a factor hundred, but still considerable, about a factor twenty-five.

Alice:

For this particular case, and also without optimization switched on. Let's try compiling both programs with the 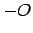$-O$ option of the g++ compiler, which should produce faster code.

|gravity> g++ -O -o leapfrog3a leapfrog3a.C
|gravity> g++ -O -o hermite2 hermite2.C
|gravity> time leapfrog3a > /dev/null
Please provide a value for the time step
0.00001
and for the duration of the run
100
Initial total energy E_in = -1.287
Final total energy E_out = -1.287
absolute energy error: E_out - E_in = -1.20237e-11
relative energy error: (E_out - E_in) / E_in = 9.34243e-12
10.690u 0.060s 0:13.94 77.1%	0+0k 0+0io 165pf+0w
|gravity> time hermite2 > /dev/null
Please provide a value for the time step
0.001
and for the duration of the run
100
Initial total energy E_in = -1.28705
Final total energy E_out = -1.28705
absolute energy error: E_out - E_in = -4.06408e-12
relative energy error: (E_out - E_in) / E_in = 3.15768e-12
0.610u 0.020s 0:02.98 21.1%	0+0k 0+0io 165pf+0w
|gravity>

Carol:

Aha! Both programs ran faster, but the leapfrog more so. Now Hermite is ahead by `only' a factor 18 or so, instead of 25.

Alice:

Still, for this particular case only. And note that the energy errors are now slightly different from before, without the optimizer switched on. Although the optimized code should in principle give the same results as the non-optimized code if there were no round-off errors, in practice round-off does creep in and propagate into the errors, especially when we are working at such high accuracies, where we are relatively few bits away from machine precisions. Fortunately, the effect does not seem to be too worrisome: we are talking about relative differences in energy error of only a few percent. But still this is something we clearly have to be aware of.

Bob:

Okay, enough warnings and footnotes! Let's call it a night. Next time we get together we'll clean up the Hermite, and make it into a general working tool.

Carol:

Sounds good! See you then.