



Next: 6.6 The Hermite Soars:
Up: 6. Exploring with a
Previous: 6.4 Implementing Hermite
[Bob:]
Now I'm ready to be brave and call the code hermite1.C. Rather
than listing the whole output, let me use the diff program,
which only lists those lines that are different.
|gravity> diff hermite1a.C hermite1.C
2c2
< // hermite1a.C
---
> // hermite1.C
30c30
< a[i][k] = jk[i][k] = 0.0;
---
> a[i][k] = 0.0;
33,34c33,34
< double rji[3], vji[3];
< for (int k = 0; k < 3; k++){
---
> double rji[3];
> for (int k = 0; k < 3; k++)
36,37d35
< vji[k] = v[j][k] - v[i][k];
< }
42,45d39
< double rv = 0;
< for (int k = 0; k < 3; k++)
< rv += rji[k] * vji[k];
< rv /= r2;
49,50d42
< jk[i][k] += m * (vji[k] - 3 * rv * rji[k]) / r3;
< jk[j][k] -= m * (vji[k] - 3 * rv * rji[k]) / r3;
64a57,81
> for (int i = 0; i < n; i++)
> for (int k = 0; k < 3; k++)
> jk[i][k] = 0.0;
> for (int i = 0; i < n; i++){
> for (int j = i+1; j < n; j++){
> double rji[3], vji[3];
> for (int k = 0; k < 3; k++){
> rji[k] = r[j][k] - r[i][k];
> vji[k] = v[j][k] - v[i][k];
> }
> double r2 = 0;
> for (int k = 0; k < 3; k++)
> r2 += rji[k] * rji[k];
> double r3 = r2 * sqrt(r2);
> double rv = 0;
> for (int k = 0; k < 3; k++)
> rv += rji[k] * vji[k];
> rv /= r2;
> for (int k = 0; k < 3; k++){
> jk[i][k] += m * (vji[k] - 3 * rv * rji[k]) / r3;
> jk[j][k] -= m * (vji[k] - 3 * rv * rji[k]) / r3;
> }
> }
> }
>
127,128d143
< r[i][k] = old_r[i][k] + (old_v[i][k] + v[i][k])*dt/2
< + (old_a[i][k] - a[i][k])*dt*dt/12;
130a146,147
> r[i][k] = old_r[i][k] + (old_v[i][k] + v[i][k])*dt/2
> + (old_a[i][k] - a[i][k])*dt*dt/12;
|gravity>
- Carol:
- Yes, that is much clearer than listing the whole source code again.
I can see how the main difference has been the move of the jerk
calculation from the earlier part, where it was entangled with the
acceleration calculation, to a separate block listed nearly at the
end. At the very end, of course, there is the indication that we have
swapped the order of the calculations of the positions and the velocities.
The diff program arbitrarily took the velocity calculation as a
identical standard in each file, with respect to which the shift in
order of the position calculation was noted.
- Alice:
- Soon we should start to clean up our codes, splitting them in
functions at least, and probably also in different files. That way we
don't have to rely on diff to read our own programs, since we
can then take natural chunks at a time, in the form of functions. But
first let's see what will happen to our figure 8 orbits.
- Bob:
- Here are the results. Hmm, not a very good energy conservation, if
you ask me.
|gravity> g++ -o hermite1 hermite1.C
|gravity> hermite1 > hermite1_0.01_100.out
Please provide a value for the time step
0.01
and for the duration of the run
100
Initial total energy E_in = -0.866025
Final total energy E_out = -1.08608
absolute energy error: E_out - E_in = -0.220054
relative energy error: (E_out - E_in) / E_in = 0.254096
|gravity>
- Carol:
- Indeed. The leapfrog did far better at this stage. We got a relative
energy error of less than
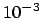 , and here we are faced with a relative
energy error of a quarter!
, and here we are faced with a relative
energy error of a quarter!
- Alice:
- That is not so strange, actually. A higher-order algorithm computes
higher-order derivatives, and therefore can be extra sensitive to
close encounters or other situations in which changes happen quite
suddenly. Let's look at the picture, and then move on, refining our
step size.
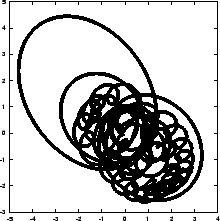
Figure 6.1:
The first Hermite attempt to integrate the orbits of three stars
starting off on a circle with an initial velocity perturbation of
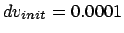 , time step
, time step 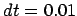 and a total duration of
and a total duration of
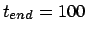
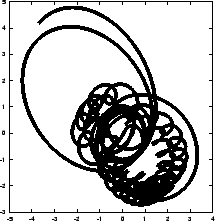 |
|gravity> hermite1 > hermite1_0.001_100.out
Please provide a value for the time step
0.001
and for the duration of the run
100
Initial total energy E_in = -0.866025
Final total energy E_out = -0.866026
absolute energy error: E_out - E_in = -9.19142e-07
relative energy error: (E_out - E_in) / E_in = 1.06133e-06
|gravity>
Figure 6.2:
The second Hermite attempt to integrate the orbits of three stars
starting off on a circle with an initial velocity perturbation of
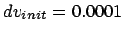 , time step
, time step 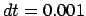 and a total duration of
and a total duration of
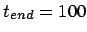
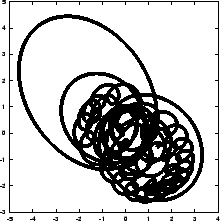 |
- Carol:
- Ah, much better! Amazing.
- Bob:
- An improvement of more than a factor 100,000 in accuracy!
- Carol:
- And look at the picture. I cannot see any difference between Fig.
6.2 and the last picture in the series that
we did with the leapfrog, Fig. 5.11!
- Alice:
- Let's take another refinement step, to see whether we can determine
the asymptotic behavior of the error growth. Clearly, our first
attempt was not reliable, so we need at least a third try.
|gravity> hermite1 > hermite1_0.0001_100.out
Please provide a value for the time step
0.0001
and for the duration of the run
100
Initial total energy E_in = -0.866025
Final total energy E_out = -0.866025
absolute energy error: E_out - E_in = -8.49854e-12
relative energy error: (E_out - E_in) / E_in = 9.81326e-12
|gravity>
Figure 6.3:
The third Hermite attempt to integrate the orbits of three stars
starting off on a circle with an initial velocity perturbation of
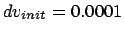 , time step
, time step 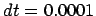 and a total duration of
and a total duration of
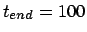
 |
- Carol:
- Okay, Bob, you can call this code hermite1.C, it seems to do its job.
- Bob:
- But it does its job too well. Another five magnitudes of error improvement.
Now it behaves like a fifth order code.
- Alice:
- This seems to happen sometimes. A
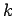 th-order scheme is guaranteed
only to have errors that grow not faster than
th-order scheme is guaranteed
only to have errors that grow not faster than 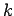 th order. However,
it is possible for them to grow less fast. For example, it could be
that the particular orbits we are studying just happen to have some
properties that lead to cancellations in some of the orders.
th order. However,
it is possible for them to grow less fast. For example, it could be
that the particular orbits we are studying just happen to have some
properties that lead to cancellations in some of the orders.
- Carol:
- Is there any reason to believe that we do not have a generic system here?
- Alice:
- Don't forget that we are studying a rather unstable system, in which
it is quite likely that we will have at least one close encounter
between two or three particles. So far, we have been sailing blindly,
hoping that the step size we give the integrator is small enough to
prevent near-collisions or other forms of strange behavior during
close encounters. Soon we'll have to do better, though. It is not
too hard to predict close encounters when they are about to happen,
and to adapt the integration step size automatically. Only with such
safety precautions does it make sense to rigorously measure the
performance of the algorithm, whether it is the leapfrog or the
Hermite. Without such precautions, even slight changes could show a
different behavior. For example, cleaning up the code by initializing
the velocities directly, instead of using the centrifugal trick, is
likely to give slightly different initial conditions. I would not
be surprised if such a change gave us yet another scaling of the
errors, if we repeat the above measurements.
- Bob:
- Okay, I guess we are ready to do quite a bit of cleaning up in our code.
It is getting a bit too spaghetti-like for my taste already. Let's do
that next time. We can improve readability and functionality at the
same time, while we go along.
- Carol:
- For now though, I feel that the Hermite should be our tool of choice.
It sure seems to converge must faster. How about doing a timing test?
- Bob:
- Good idea. Let's do it with the figure-8 orbits though. There at
least we do not have any close encounters, so Alice's warnings may
carry less urgency.




Next: 6.6 The Hermite Soars:
Up: 6. Exploring with a
Previous: 6.4 Implementing Hermite
The Art of Computational Science
2004/01/25


