



Next: 11.2 Finding Binaries
Up: 11. Fishing for Binaries
Previous: 11. Fishing for Binaries
The next day, our three friends get together again. Alice looks a bit
sleepy, obviously has stayed up late the previous night.
- Carol:
- Fortunately, we have a blackboard in this room.
- Bob:
- And more important, we have Alice in the room!
- Alice:
- But only a half-awake Alice. Yesterday evening it took me longer than
I thought to figure everything out. What I found looks easy, it always
does in the end, but I didn't realize how much I had forgotten about
the classical dynamics course that I had followed in my freshman year.
- Bob:
- Some day I'd like to know how you derived whatever you derived, but
for now, I'm really eager to fish for binaries, so let's not worry too
much about derivations. Perhaps you can just show us what you found.
- Carol:
- I second that. Let's see whether it works first, and if it turns out
to be useful, I'd love to learn more about the details.
- Alice:
- Fine with me, and just as well, since I don't think I'm quite together
enough to give a complete pedagogical derivation.
Alice walks to the blackboard, and writes down the equations for the
energy 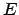 and angular momentum
and angular momentum 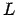 for a two-body system. Here the
masses of the two bodies are
for a two-body system. Here the
masses of the two bodies are 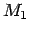 and
and 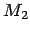 . The relative position
vector, pointing from
. The relative position
vector, pointing from 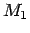 to
to 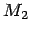 , is given by
, is given by 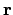 , and its time
derivative is the relative velocity vector
, and its time
derivative is the relative velocity vector 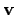 . As before,
. As before, 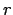 is
the absolute value of
is
the absolute value of 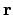 , a scalar, equal to the length of the
vector
, a scalar, equal to the length of the
vector 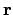 , and similar
, and similar 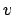 is the length of
is the length of 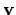 . The energy is
given by the sum of the negative potential energy and the positive
kinetic energy. The angular momentum points along the outer product,
also called the cross product, of the relative position and velocity
vectors. This implies that it points in a direction perpendicular to
the orbit of the two bodies.
. The energy is
given by the sum of the negative potential energy and the positive
kinetic energy. The angular momentum points along the outer product,
also called the cross product, of the relative position and velocity
vectors. This implies that it points in a direction perpendicular to
the orbit of the two bodies.
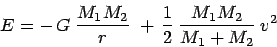 |
(11.1) |
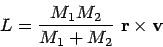 |
(11.2) |
Note that we could have defined 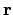 equally well as pointing from
equally well as pointing from
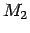 to
to 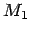 , as long as
, as long as 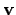 would still be the time derivative of
would still be the time derivative of
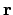 . In the definition of the energy, the lengths of
. In the definition of the energy, the lengths of 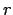 and
and 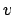 would not change, and in the definition of the angular momentum, the
two minus signs that would thus be introduced at the right would
cancel each other.
would not change, and in the definition of the angular momentum, the
two minus signs that would thus be introduced at the right would
cancel each other.
These equations simplify considerably when we introducing the symbol
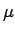 for the reduced mass, defined as follows:
for the reduced mass, defined as follows:
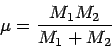 |
(11.3) |
we can now write the energy per unit of reduced mass as
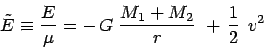 |
(11.4) |
and similarly the angular momentum per unit of reduced mass as
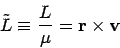 |
(11.5) |
- Alice:
- The shape of a binary orbit is given by the values of the semi-major
axis
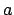 and the eccentricity
and the eccentricity 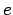 . We can find those values in two steps.
First we invert the expression that gives
. We can find those values in two steps.
First we invert the expression that gives 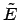 in terms of
in terms of 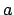 ,
to obtain an expression for
,
to obtain an expression for 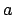 :
:
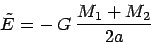 |
(11.6) |
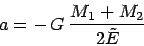 |
(11.7) |
- Alice:
- And similarly, we invert the expression that gives
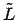 in terms
of
in terms
of 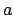 and
and 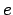 , to obtain an expression for
, to obtain an expression for 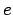 , or to keep it simple,
for
, or to keep it simple,
for 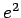 (we can always take the square root later):
(we can always take the square root later):
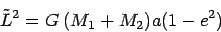 |
(11.8) |
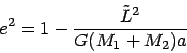 |
(11.9) |
- Alice:
- The interpretation is as follows: as the name suggests,
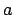 is half
the length of the longest axis of the ellipse that describes the
relative orbit of the two bodies; in this way
is half
the length of the longest axis of the ellipse that describes the
relative orbit of the two bodies; in this way 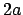 is size of the orbit.
The eccentricity
is size of the orbit.
The eccentricity 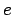 indicates the relative displacement of the focus
of the orbit from the center of the orbit. The closest approach
between the two bodies occurs at a distance of
indicates the relative displacement of the focus
of the orbit from the center of the orbit. The closest approach
between the two bodies occurs at a distance of 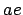 , also called the
pericenter distance, while the largest separation occurs at a distance
of
, also called the
pericenter distance, while the largest separation occurs at a distance
of 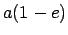 , the apocenter distance.
, the apocenter distance.




Next: 11.2 Finding Binaries
Up: 11. Fishing for Binaries
Previous: 11. Fishing for Binaries
The Art of Computational Science
2004/01/25
![]() and angular momentum
and angular momentum ![]() for a two-body system. Here the
masses of the two bodies are
for a two-body system. Here the
masses of the two bodies are ![]() and
and ![]() . The relative position
vector, pointing from
. The relative position
vector, pointing from ![]() to
to ![]() , is given by
, is given by ![]() , and its time
derivative is the relative velocity vector
, and its time
derivative is the relative velocity vector ![]() . As before,
. As before, ![]() is
the absolute value of
is
the absolute value of ![]() , a scalar, equal to the length of the
vector
, a scalar, equal to the length of the
vector ![]() , and similar
, and similar ![]() is the length of
is the length of ![]() . The energy is
given by the sum of the negative potential energy and the positive
kinetic energy. The angular momentum points along the outer product,
also called the cross product, of the relative position and velocity
vectors. This implies that it points in a direction perpendicular to
the orbit of the two bodies.
. The energy is
given by the sum of the negative potential energy and the positive
kinetic energy. The angular momentum points along the outer product,
also called the cross product, of the relative position and velocity
vectors. This implies that it points in a direction perpendicular to
the orbit of the two bodies.
![]() equally well as pointing from
equally well as pointing from
![]() to
to ![]() , as long as
, as long as ![]() would still be the time derivative of
would still be the time derivative of
![]() . In the definition of the energy, the lengths of
. In the definition of the energy, the lengths of ![]() and
and ![]() would not change, and in the definition of the angular momentum, the
two minus signs that would thus be introduced at the right would
cancel each other.
would not change, and in the definition of the angular momentum, the
two minus signs that would thus be introduced at the right would
cancel each other.
![]() for the reduced mass, defined as follows:
for the reduced mass, defined as follows: