11.2 Finding Binaries

Carol:

Thanks, Alice, let's code it up.

While Bob and Alice look on, and occasionally give some comments, Carol produces the following code. First, she summarized the structure and usage:

followed by the usual include stuff and declarations, etc.:

The main part of the code is rather simple: one by one the snapshots are read in and a search for binaries is done, by invoking the function find_binaries:

There are no command line arguments, apart from the standard help option:

We have seen before how to read in a snapshot:

Also, we have seen before how to delete in a snapshot once it is no longer needed:

Finally, here is the code where the real work is done. The equations written above are used directly to find and report the values for the semi-major axis 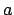$a$ and eccentricity 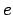$e$. Each particle pair that has a negative relative energy is considered to be a bound system, in other words a binary:

Bob:

I'm really curious now what will happen. How about starting carefully, in a number of easy steps, since we're entering new and unknown terrain here.

Carol:

Now you begin to talk like a computer scientist! But I agree, let's feel our way around, to make sure we understand what we're doing.

Alice:

The obvious first step would be to look at the output of sphere1.C, to see whether there would be any binaries already present.

Bob:

Let's choose a particle seed, so that we can reproduce our results.

|gravity> ../chap9/sphere1 -s 42 -n 25 | find_binaries1
seed = 42
time = 0
star1 = 0  star2 = 1  a = 0.856428  e = 1
star1 = 0  star2 = 2  a = 0.397074  e = 1
star1 = 0  star2 = 3  a = 0.331345  e = 1
 . . . .
star1 = 22  star2 = 23  a = 0.683746  e = 1
star1 = 22  star2 = 24  a = 0.562686  e = 1
star1 = 23  star2 = 24  a = 0.330094  e = 1
|gravity>

Carol:

Wow, that went by too quick, but there sure were a lot of so-called binaries. How many were there altogether?

Bob:

Let see. Here is the answer:

|gravity> ../chap9/sphere1 -s 42 -n 25 | find_binaries1 | wc
seed = 42
    301    3603   12941
|gravity>

Bob:

We know that there is a line time = 0, so if we leave that line out, we realize that we have just found a grand total of 300 binaries. And all that with only 25 stars ?!?

Alice:

I see what the problem is. We begin with a cold start, remember? All velocities are set equal to zero, initially.

Carol:

So this means the kinetic energy of any and every pair of stars is identically zero.

Bob:

And therefore the total energy is negative, since potential energy is always negative. So we should have found 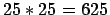$25 * 25 = 625$ binaries, no?

Alice:

You can't be a binary with yourself, so there are only 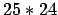$25 * 24$ candidates. However, that still leaves us with 600 binaries.

Carol:

Ah, but remember, I tested each pair only once, independent of whether I started with the first or the second star. In other words, for the first star, I did 24 tests with all other stars; for the second star I needed only to test binarity with respect to the other 23 stars; and so on, until the next-to-last star only had to be tested with respect to the last star, and we were done. This means that there are only 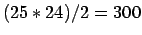$(25*24)/2 = 300$ star pairs that were tested.

Bob:

Indeed just what we found. Phew, I'm relieved. At least the output makes sense, even this is not quite what we intended.

Alice:

Notice the typical semi-major axis values in our output: all these binary-wanna-be systems claim to have 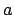$a$ values spread more or less equally between 0 and 1. In practice, any stable binary would have an orbit far smaller than the size of the system.

Carol:

How about adding an option to the code through which we exclude all binaries that are larger than a certain cut-off value?

Bob:

That should help, yes, let's try that.