11.3 Finding Tight Binaries

Bob and Alice again watch Carol, who quickly copies the file find_binaries1.C to a new file find_binaries2.C, and then starts editing the new file, in order to add a cut-off option.

Carol:

Here is the new main part. As you can see, I have added the cut-off value a_max for the semi-major axis of the binaries to be reported as an optional argument. Running find_binaries2.C in the same way as find_binaries1.C should give the same output, since the default cutoff is a VERY_LARGE_NUMBER, in our case equal to 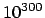$10^{300}$, which means that no binary found will be rejected.

Here the option is added to the parsing of the command line argument:

And here the extra test is implemented in the actual search routine.

Bob:

Let's try to see first whether your claim is correct, that find_binaries2.C gives the same output as find_binaries1.C.

Carol:

Okay, here is the word count:

|gravity> ../chap9/sphere1 -s 42 -n 25 | find_binaries2 | wc
seed = 42
    301    3603   12941
|gravity>

Carol:

And to make really sure, here is a diff between the two outputs:

|gravity> ../chap9/sphere1 -s 42 -n 25 | find_binaries1 > tmp1
seed = 42
|gravity> ../chap9/sphere1 -s 42 -n 25 | find_binaries2 > tmp2
seed = 42
|gravity> diff tmp1 tmp2
|gravity>

Bob:

I'm convinced! Now what shall we choose for a_max? How about $a_{max} = 0.1$?

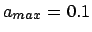Carol:

Fine, but let's start with a word count.

|gravity> ../chap9/sphere1 -s 42 -n 25 | find_binaries2 -a 0.1 | wc
seed = 42
      4      39     142
|gravity>

Bob:

A lot better already. Discounting again the line time = 0, we have found 3 tight binaries.

Alice:

But even those binaries are likely to be not physical, but just chance positionings of two particles that happen to be within a distance of 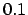$0.1$ of each other, in our units. Since the velocities are zero, any particle pair that close will be counted. We have only shown that 3 out of 300 pairs are this close, just 1% of the possible pair choices.

Bob:

I would have expected something like 0.1%, one in a thousand, since the room each particle has for harboring a neighbor at such a small distance is the volume of a sphere with radius 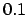$0.1$. And in three dimensions that volume is a thousand times smaller than the volume of the sphere in which particles are located, which has radius unity.

Carol:

Ah, but there are 25 particles that you can start with; what you just derived was the chance to find a binary companion around a particular star.

Alice:

And then we have to divide by two to avoid each pair from being counted twice. So we wind up with an estimate of 1.25%, so we could have expected 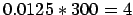$0.0125*300=4$ stars, on average. To find 3 seems close enough.

Bob:

Here are a few more, now for random seeds

|gravity> ../chap9/sphere1 -n 25 | find_binaries2 -a 0.1 | wc
seed = 1064763074
      5      51     184
|gravity>  !!
../chap9/sphere1 -n 25 | find_binaries2 -a 0.1 | wc
seed = 1064763076
      4      39     142
|gravity>  !!
../chap9/sphere1 -n 25 | find_binaries2 -a 0.1 | wc
seed = 1064763078
      3      27      98
|gravity>  !!
../chap9/sphere1 -n 25 | find_binaries2 -a 0.1 | wc
seed = 1064763082
      3      27      97
|gravity>  !!
../chap9/sphere1 -n 25 | find_binaries2 -a 0.1 | wc
seed = 1064763084
      6      63     230
|gravity>  !!
../chap9/sphere1 -n 25 | find_binaries2 -a 0.1 | wc
seed = 1064763087
      3      27      98
|gravity>  !!
../chap9/sphere1 -n 25 | find_binaries2 -a 0.1 | wc
seed = 1064763090
      5      51     187
|gravity>  !!
../chap9/sphere1 -n 25 | find_binaries2 -a 0.1 | wc
seed = 1064763093
      4      39     140
|gravity>  !!
../chap9/sphere1 -n 25 | find_binaries2 -a 0.1 | wc
seed = 1064763097
      3      27      99
|gravity>  !!
../chap9/sphere1 -n 25 | find_binaries2 -a 0.1 | wc
seed = 1064763098
      4      39     142
|gravity>  
|gravity>

Bob:

The average is still 3, not 4. In any case, statistics is a very tricky subject, and I wouldn't be surprised if the true value would be slightly different from our rough estimate of 4. For example, there may be edge effects involved, for particles near the surface of the sphere. But I would be uncomfortable if the outcome had been vastly different from 4 on average.

Alice:

Now that we're happy with the statistics, can you show the actual output?

Bob:

Ah, of course, here it is:

|gravity> ../chap9/sphere1 -s 42 -n 25 | find_binaries2 -a 0.1
seed = 42
time = 0
star1 = 6  star2 = 12  a = 0.0271531  e = 1
star1 = 8  star2 = 23  a = 0.0783721  e = 1
star1 = 13  star2 = 14  a = 0.0386034  e = 1
|gravity>

Bob:

Looks pretty random to me. And the eccentricities are all unity, as I should have predicted, had I thought about it, given that the velocities are zero. Particles falling toward each other move on a straight line, the extreme case of an ellipse with eccentricity 1.