11.4 Dynamically Produced Binaries

Carol:

Why don't we do a real run now.

Bob:

I'll use our workhorse, nbody_sh1.C with options -i to include output for time 0 as well, and -e 10 to allow only energy diagnostics at the beginning and at the end so as not to clutter the screen.

|gravity> ../chap9/sphere1 -s 42 -n 25 | ../chap8/nbody_sh1 -e 10 -i | find_binaries2 -a 0.1
seed = 42
Starting a Hermite integration for a 25-body system,
  from time t = 0 with time step control parameter dt_param = 0.03  until time 10 ,
  with diagnostics output interval dt_dia = 10,
  and snapshot output interval dt_out = 1.
at time t = 0 , after 0 steps :
  E_kin = 0 , E_pot = -0.61885 , E_tot = -0.61885
                absolute energy error: E_tot - E_init = 0
                relative energy error: (E_tot - E_init) / E_init = -0
time = 0
star1 = 6  star2 = 12  a = 0.0271531  e = 1
star1 = 8  star2 = 23  a = 0.0783721  e = 1
star1 = 13  star2 = 14  a = 0.0386034  e = 1
time = 1.00008
star1 = 16  star2 = 21  a = 0.0601398  e = 0.612398
time = 2.00009
star1 = 1  star2 = 3  a = 0.0816514  e = 0.823595
star1 = 1  star2 = 4  a = 0.0200926  e = 0.945035
star1 = 5  star2 = 8  a = 0.0336744  e = 0.798637
star1 = 8  star2 = 23  a = 0.00884901  e = 0.744231
time = 3.00005
star1 = 0  star2 = 1  a = 0.048932  e = 0.926806
star1 = 0  star2 = 21  a = 0.0669483  e = 0.681452
star1 = 1  star2 = 3  a = 0.0668783  e = 0.994049
star1 = 1  star2 = 21  a = 0.041487  e = 0.87713
star1 = 5  star2 = 8  a = 0.0541946  e = 0.841467
star1 = 5  star2 = 23  a = 0.00772702  e = 0.905568
time = 4.00008
star1 = 0  star2 = 3  a = 0.080123  e = 0.872677
star1 = 0  star2 = 21  a = 0.0268892  e = 0.940599
star1 = 2  star2 = 11  a = 0.0061008  e = 0.807254
star1 = 2  star2 = 19  a = 0.0910958  e = 0.653393
time = 5.00001
star1 = 2  star2 = 19  a = 0.0226411  e = 0.927754
star1 = 3  star2 = 21  a = 0.0149472  e = 0.595139
star1 = 5  star2 = 17  a = 0.00895071  e = 0.422472
time = 6.00001
star1 = 2  star2 = 19  a = 0.0023379  e = 0.508743
star1 = 3  star2 = 21  a = 0.0159819  e = 0.556314
time = 7.00001
star1 = 0  star2 = 21  a = 0.0180656  e = 0.303921
star1 = 2  star2 = 19  a = 0.00233757  e = 0.507285
time = 8.00002
star1 = 0  star2 = 4  a = 0.0258779  e = 0.996719
star1 = 0  star2 = 21  a = 0.0279722  e = 0.883476
star1 = 2  star2 = 19  a = 0.00233754  e = 0.507268
star1 = 4  star2 = 21  a = 0.0805251  e = 0.390524
time = 9.00001
star1 = 0  star2 = 21  a = 0.0132626  e = 0.650153
star1 = 2  star2 = 19  a = 0.0023375  e = 0.506389
at time t = 10 , after 498929 steps :
  E_kin = 0.672558 , E_pot = -1.1658 , E_tot = -0.493243
                absolute energy error: E_tot - E_init = 0.125607
                relative energy error: (E_tot - E_init) / E_init = -0.202968
time = 10
star1 = 0  star2 = 3  a = 0.0243207  e = 0.965155
star1 = 0  star2 = 21  a = 0.0311286  e = 0.764542
star1 = 2  star2 = 19  a = 0.00233747  e = 0.506845
star1 = 3  star2 = 21  a = 0.0458811  e = 0.746161
|gravity>

Bob:

I'm glad to see that only at time 0 we have those skinny binaries with eccentricity 0. And hey, look at that very tight binary, with a semi-major axis of only 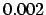$0.002$, formed by stars 2 and 19!

Carol:

It is clearly a persistent binary. It was already there at time 6, with pretty much the same short semi-major axis.

Alice:

Once a binary is so tight, it is less likely that any other star will come close to that close pair, so it will take a long time before there is another strong interaction.

Bob:

I see what you mean: the same binary was present at time 5, but with a much wider orbit, about ten times as large; and it did not last long at that larger distance, before it got a lot tighter.

Alice:

That event must have been a more complex three-body dance. You can see that at time 4, star 2 was simultaneously considered to be bound to start 19 and to star 11. It was far closer to start 11 at that time, so the large binding energy must have come at least partly from that pair.

Bob:

Ho! Before we analyze much further, I just noticed something really bad. In our excitement about binaries, we forgot to check whether the energy conservation was reasonable. Look! We have a relative energy error of more than 20%.

Carol:

That's no good. We should rerun with a smaller accuracy parameter for the integrator.

Alice:

I agree. Still, the main points we made are likely to remain valid qualitatively, even if not quantitatively.

Bob:

I'll use the same seed again, but with a three times smaller step size control parameter. With a fourth-order integration scheme, that should reduce the relative energy error for the whole system to much less than 1%.

|gravity> ../chap9/sphere1 -s 42 -n 25 | ../chap8/nbody_sh1 -d 0.01 -e 10 -i | find_binaries2 -a 0.1
seed = 42
Starting a Hermite integration for a 25-body system,
  from time t = 0 with time step control parameter dt_param = 0.01  until time 10 ,
  with diagnostics output interval dt_dia = 10,
  and snapshot output interval dt_out = 1.
at time t = 0 , after 0 steps :
  E_kin = 0 , E_pot = -0.61885 , E_tot = -0.61885
                absolute energy error: E_tot - E_init = 0
                relative energy error: (E_tot - E_init) / E_init = -0
time = 0
star1 = 6  star2 = 12  a = 0.0271531  e = 1
star1 = 8  star2 = 23  a = 0.0783721  e = 1
star1 = 13  star2 = 14  a = 0.0386034  e = 1
time = 1.00008
star1 = 5  star2 = 18  a = 0.0804608  e = 0.373533
star1 = 7  star2 = 16  a = 0.0653846  e = 0.980501
star1 = 14  star2 = 16  a = 0.0592383  e = 0.88506
time = 2.00006
star1 = 7  star2 = 15  a = 0.0551175  e = 0.78881
star1 = 8  star2 = 10  a = 0.082922  e = 0.406961
time = 3.00003
star1 = 8  star2 = 13  a = 0.00555818  e = 0.849134
star1 = 10  star2 = 16  a = 0.0420807  e = 0.772984
star1 = 10  star2 = 19  a = 0.0345081  e = 0.967946
time = 4
star1 = 3  star2 = 10  a = 0.0645721  e = 0.651257
star1 = 7  star2 = 23  a = 0.0778391  e = 0.475478
star1 = 8  star2 = 13  a = 0.00554977  e = 0.677847
time = 5
star1 = 3  star2 = 8  a = 0.002126  e = 0.920892
star1 = 4  star2 = 22  a = 0.0423633  e = 0.638268
time = 6
star1 = 3  star2 = 8  a = 0.00212601  e = 0.952222
star1 = 4  star2 = 22  a = 0.0403322  e = 0.827227
time = 7
star1 = 3  star2 = 8  a = 0.00220527  e = 0.777804
time = 8
star1 = 3  star2 = 8  a = 0.00220456  e = 0.732745
time = 9
star1 = 3  star2 = 8  a = 0.00197343  e = 0.801175
at time t = 10 , after 2642122 steps :
  E_kin = 0.783526 , E_pot = -0.871684 , E_tot = -0.0881583
                absolute energy error: E_tot - E_init = 0.530692
                relative energy error: (E_tot - E_init) / E_init = -0.857545
time = 10
star1 = 3  star2 = 8  a = 0.00197342  e = 0.806924
|gravity>

Bob:

What happened? I had expected it to take three times longer, with a three times smaller step size criterion; instead it took five times longer, with more than two and a half million steps instead of the previous half million. And what is worse, the energy conservation is now atrocious!

Alice:

The fact that we have embarked on a completely different history is by itself not surprising. The 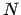$N$-body system is exponentially unstable. In other words, even a slight chance anywhere in the position or velocity of any single particle will quickly lead to a completely different behavior of the system. This is what is popularly called the butterfly effect: if a butterfly flaps its wings somewhere in the world, and if that happens in an exponentially unstable part of a weather zone, the whole weather pattern on the planet could become rather different after a few weeks or so from what it otherwise would have been. Whether this is really true for actual butterflies, I don't know, but it is certainly true for stars!

Carol:

So we may have just been unlucky, getting not only onto a different trajectory, but on a trajectory with a bad energy behavior to boot. But a few days ago, we had much better luck with energy conservation. How about trying again, but actually degrading the accuracy a bit, with the option -a 0.02, in between the default of -a 0.03 and the -a 0.01 you just tried? Who knows, we may be more lucky this time.

Bob:

Using a Monte Carlo method? I didn't think playing roulette was a very scientific approach! But what the heck, let's give it a try.

Alice:

You may not have heard of it, but there is actually something called a Monte Carlo method in science! If we had chosen a rejection technique to construct our homogeneous spherical particle distribution, we would have used a type of Monte Carlo technique.

Bob:

What do you know. Well, why don't we call Carol's proposed hit-and-miss approach a Monte Carol method.

Carol:

You'd better start typing instead!

|gravity> ../chap9/sphere1 -s 42 -n 25 | ../chap8/nbody_sh1 -d 0.01 -e 10 -i | find_binaries2 -a 0.1
|gravity> ../chap9/sphere1 -s 42 -n 25 | ../chap8/nbody_sh1 -d 0.02 -e 10 -i | find_binaries2 -a 0.1
seed = 42
Starting a Hermite integration for a 25-body system,
  from time t = 0 with time step control parameter dt_param = 0.02  until time 10 ,
  with diagnostics output interval dt_dia = 10,
  and snapshot output interval dt_out = 1.
at time t = 0 , after 0 steps :
  E_kin = 0 , E_pot = -0.61885 , E_tot = -0.61885
                absolute energy error: E_tot - E_init = 0
                relative energy error: (E_tot - E_init) / E_init = -0
time = 0
star1 = 6  star2 = 12  a = 0.0271531  e = 1
star1 = 8  star2 = 23  a = 0.0783721  e = 1
star1 = 13  star2 = 14  a = 0.0386034  e = 1
time = 1.00047
star1 = 5  star2 = 18  a = 0.0810243  e = 0.423949
star1 = 7  star2 = 14  a = 0.0492761  e = 0.914931
time = 2.00002
star1 = 2  star2 = 3  a = 0.084026  e = 0.496036
star1 = 7  star2 = 14  a = 0.068698  e = 0.706102
star1 = 17  star2 = 19  a = 0.0137171  e = 0.782917
time = 3.00001
star1 = 0  star2 = 19  a = 0.0336442  e = 0.813088
star1 = 4  star2 = 17  a = 0.0157056  e = 0.832995
star1 = 7  star2 = 21  a = 0.0377602  e = 0.835347
star1 = 17  star2 = 18  a = 0.0190899  e = 0.891115
time = 4.00003
star1 = 3  star2 = 10  a = 0.0363436  e = 0.795917
star1 = 5  star2 = 19  a = 0.0861304  e = 0.614849
star1 = 7  star2 = 21  a = 0.0377828  e = 0.83908
star1 = 10  star2 = 17  a = 0.0491587  e = 0.319343
time = 5.00006
star1 = 4  star2 = 18  a = 0.049268  e = 0.70185
star1 = 7  star2 = 21  a = 0.0377876  e = 0.839173
star1 = 8  star2 = 24  a = 0.0812205  e = 0.513454
time = 6.00001
star1 = 4  star2 = 17  a = 0.0142633  e = 0.783939
star1 = 7  star2 = 21  a = 0.0377902  e = 0.838337
star1 = 8  star2 = 24  a = 0.0252418  e = 0.941765
star1 = 17  star2 = 24  a = 0.0727696  e = 0.719213
time = 7.00001
star1 = 4  star2 = 13  a = 0.00581595  e = 0.110655
star1 = 7  star2 = 21  a = 0.0377915  e = 0.836602
time = 8.00002
star1 = 4  star2 = 13  a = 0.00627755  e = 0.258843
star1 = 7  star2 = 21  a = 0.0377902  e = 0.831768
time = 9.00014
star1 = 4  star2 = 23  a = 0.0182906  e = 0.961251
star1 = 7  star2 = 21  a = 0.033901  e = 0.86658
star1 = 13  star2 = 15  a = 0.0571123  e = 0.45941
star1 = 13  star2 = 23  a = 0.0455079  e = 0.890129
at time t = 10 , after 300848 steps :
  E_kin = 0.811683 , E_pot = -0.997429 , E_tot = -0.185746
                absolute energy error: E_tot - E_init = 0.433104
                relative energy error: (E_tot - E_init) / E_init = -0.699853
time = 10
star1 = 4  star2 = 8  a = 0.00255213  e = 0.988263
star1 = 7  star2 = 21  a = 0.0340237  e = 0.880843
star1 = 8  star2 = 24  a = 0.0435369  e = 0.365145
|gravity>

Bob:

No cigar. Yes, a completely different run, but no, still a bad energy behavior. By now I'm getting pretty curious to see how and when this bad energy error occurs. Let's get some more information, once every unit time increase.

|gravity> ../chap9/sphere1 -s 42 -n 25 | ../chap8/nbody_sh1 -d 0.02 > /dev/null
seed = 42
Starting a Hermite integration for a 25-body system,
  from time t = 0 with time step control parameter dt_param = 0.02  until time 10 ,
  with diagnostics output interval dt_dia = 1,
  and snapshot output interval dt_out = 1.
at time t = 0 , after 0 steps :
  E_kin = 0 , E_pot = -0.61885 , E_tot = -0.61885
                absolute energy error: E_tot - E_init = 0
                relative energy error: (E_tot - E_init) / E_init = -0
at time t = 1.00047 , after 12485 steps :
  E_kin = 1.06276 , E_pot = -1.24842 , E_tot = -0.185664
                absolute energy error: E_tot - E_init = 0.433187
                relative energy error: (E_tot - E_init) / E_init = -0.699986
at time t = 2.00002 , after 21245 steps :
  E_kin = 1.14737 , E_pot = -1.33303 , E_tot = -0.185664
                absolute energy error: E_tot - E_init = 0.433187
                relative energy error: (E_tot - E_init) / E_init = -0.699986
at time t = 3.00001 , after 30349 steps :
  E_kin = 1.20407 , E_pot = -1.38973 , E_tot = -0.185664
                absolute energy error: E_tot - E_init = 0.433186
                relative energy error: (E_tot - E_init) / E_init = -0.699986
^d
|gravity>

Carol:

That was a good move, Bob! So the error started right away. How strange. Could you make the energy output interval even shorter?

Bob:

I'll make it a hundred times shorter. See what happens

|gravity> ../chap9/sphere1 -s 42 -n 25 | ../chap8/nbody_sh1 -e 0.01 -d 0.02 > /dev/null
seed = 42
Starting a Hermite integration for a 25-body system,
  from time t = 0 with time step control parameter dt_param = 0.02  until time 10 ,
  with diagnostics output interval dt_dia = 0.01,
  and snapshot output interval dt_out = 1.
at time t = 0 , after 0 steps :
  E_kin = 0 , E_pot = -0.61885 , E_tot = -0.61885
                absolute energy error: E_tot - E_init = 0
                relative energy error: (E_tot - E_init) / E_init = -0
at time t = 0.0106043 , after 12 steps :
  E_kin = 0.00111979 , E_pot = -0.61997 , E_tot = -0.61885
                absolute energy error: E_tot - E_init = 4.737e-10
                relative energy error: (E_tot - E_init) / E_init = -7.65452e-10
at time t = 0.0203781 , after 24 steps :
  E_kin = 0.00454037 , E_pot = -0.62339 , E_tot = -0.61885
                absolute energy error: E_tot - E_init = 6.01715e-10
                relative energy error: (E_tot - E_init) / E_init = -9.72311e-10
at time t = 0.0304865 , after 39 steps :
  E_kin = 0.0123603 , E_pot = -0.63121 , E_tot = -0.61885
                absolute energy error: E_tot - E_init = 7.24435e-10
                relative energy error: (E_tot - E_init) / E_init = -1.17062e-09
at time t = 0.0400792 , after 60 steps :
  E_kin = 0.0317015 , E_pot = -0.650552 , E_tot = -0.61885
                absolute energy error: E_tot - E_init = 3.93875e-11
                relative energy error: (E_tot - E_init) / E_init = -6.36463e-11
at time t = 0.0500072 , after 1790 steps :
  E_kin = 0.399428 , E_pot = -1.13502 , E_tot = -0.735588
                absolute energy error: E_tot - E_init = -0.116738
                relative energy error: (E_tot - E_init) / E_init = 0.188638
at time t = 0.0600297 , after 3663 steps :
  E_kin = 0.55247 , E_pot = -0.738132 , E_tot = -0.185662
                absolute energy error: E_tot - E_init = 0.433188
                relative energy error: (E_tot - E_init) / E_init = -0.699989
|gravity>

Alice:

Ah, a bad seed, so to speak. Something dramatic happened already within the first one tenth of the first time unit!

Carol:

It would be interesting to find out more about what happened, and we do have the tools to do so, armed as we are with movie making equipment and a binary detector. We could even write a close encounter detector, similar to the binary detector but then for unbounded hyperbolic orbits. Perhaps they were the culprit.

Bob:

All nice and fine, but first things first. Let me just take a different seed, and finally get a decent 25-body evolution, to see what our binary detector does under less pathological circumstances.

|gravity> ../chap9/sphere1 -s 43 -n 25 | ../chap8/nbody_sh1 -e 10 -i | find_binaries2 -a 0.1
seed = 43
Starting a Hermite integration for a 25-body system,
  from time t = 0 with time step control parameter dt_param = 0.03  until time 10 ,
  with diagnostics output interval dt_dia = 10,
  and snapshot output interval dt_out = 1.
at time t = 0 , after 0 steps :
  E_kin = 0 , E_pot = -0.569576 , E_tot = -0.569576
                absolute energy error: E_tot - E_init = 0
                relative energy error: (E_tot - E_init) / E_init = -0
time = 0
star1 = 3  star2 = 6  a = 0.0653857  e = 1
star1 = 10  star2 = 23  a = 0.0388408  e = 1
time = 1.00015
star1 = 6  star2 = 13  a = 0.0631629  e = 0.403642
star1 = 10  star2 = 17  a = 0.0668875  e = 0.452269
time = 2.00015
star1 = 6  star2 = 13  a = 0.0413988  e = 0.918359
star1 = 12  star2 = 22  a = 0.0335088  e = 0.255619
star1 = 17  star2 = 18  a = 0.0773984  e = 0.823559
time = 3.00008
star1 = 0  star2 = 22  a = 0.0906416  e = 0.924285
star1 = 4  star2 = 12  a = 0.0261997  e = 0.596176
star1 = 6  star2 = 13  a = 0.0417364  e = 0.86777
star1 = 10  star2 = 16  a = 0.0706447  e = 0.835167
time = 4.0002
star1 = 4  star2 = 22  a = 0.0858038  e = 0.739406
star1 = 4  star2 = 23  a = 0.0933074  e = 0.730645
star1 = 6  star2 = 13  a = 0.0415368  e = 0.860736
time = 5.00032
star1 = 4  star2 = 22  a = 0.0151778  e = 0.983233
star1 = 18  star2 = 23  a = 0.0982301  e = 0.754695
time = 6.00013
star1 = 3  star2 = 10  a = 0.0345493  e = 0.752254
time = 7.00037
star1 = 3  star2 = 4  a = 0.0726365  e = 0.907422
star1 = 3  star2 = 17  a = 0.0738742  e = 0.856752
star1 = 4  star2 = 17  a = 0.0742944  e = 0.94384
time = 8.00001
star1 = 1  star2 = 8  a = 0.0341744  e = 0.990472
star1 = 22  star2 = 23  a = 0.0467334  e = 0.70404
time = 9.00015
star1 = 0  star2 = 4  a = 0.0548707  e = 0.917466
star1 = 3  star2 = 4  a = 0.0186082  e = 0.237707
star1 = 3  star2 = 8  a = 0.0681921  e = 0.993719
at time t = 10.0001 , after 54838 steps :
  E_kin = 0.490667 , E_pot = -1.06032 , E_tot = -0.569648
                absolute energy error: E_tot - E_init = -7.22701e-05
                relative energy error: (E_tot - E_init) / E_init = 0.000126884
time = 10.0001
star1 = 6  star2 = 7  a = 0.0980807  e = 0.998395
star1 = 16  star2 = 22  a = 0.0192647  e = 0.694863
|gravity>

Bob:

Hehe! That's a whole lot better. A relative energy error of about one hundredth of a percent. Perhaps a good time to stop $;>)$.

Carol:

For now, yes, but I have the feeling that we have just only uncovered the tip of an iceberg.

Alice:

I'm sure of that, too. I hope we will get back in a while, to delve further into all this.

Exercise 11.1 (Close encounters)
Design and build a piece of code similar to find_binaries2.C, but now for unbound close encounters between two particles. Use that code to analyse in more detail when and how errors become unacceptably large, as we have seen above. Can you suggest ways to improve the error accuracy, other than just setting the overall accuracy parameter to a smaller and smaller value?