Next: 4. Exploring with a
Up: 3. Exploring with a
Previous: 3.6 Finding (slow) Convergence
- Alice:
- Here are the expressions for the kinetic energy
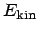 and the
potential energy
and the
potential energy 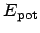 . The total energy is just the sum of
both terms.
. The total energy is just the sum of
both terms.
- Alice:
- So far, we have used units in which
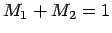 . We have not
specified the individual masses, since we did not have to; the
equations of motion are invariant with respect to how we divide our
unit of mass over the two bodies. But the interpretation in terms of
the physical energy of the system does depend on the value of
. We have not
specified the individual masses, since we did not have to; the
equations of motion are invariant with respect to how we divide our
unit of mass over the two bodies. But the interpretation in terms of
the physical energy of the system does depend on the value of 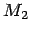 ,
which is conventionally chosen as the less massive body. Once we
choose
,
which is conventionally chosen as the less massive body. Once we
choose 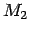 , the mass of the other body is given as
, the mass of the other body is given as 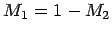 .
.
- Carol:
- I would not have guessed that the earlier invariance would be broken.
Can you make that plausible by hand waving, without deriving equations?
- Bob:
- Let me try. If we start with the Earth-Moon system, we know that the
mass of the Moon is far smaller than the mass of the Earth. Their
mass ratio is roughly 1 : 81, so the Moon has not much more than one
percent of the Earth's mass. In our notation,
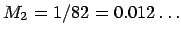 . In the center-of-mass system, the
velocities of the two bodies are inversely proportional to their
masses. Kinetic energy, however, is proportional to the square of the
velocities, and therefore the motion of the Moon carries about 81
times more kinetic energy than the motion of the Earth, around their
common center of gravity -- which lies inside the Earth, by the way,
so the Earth barely moves.
. In the center-of-mass system, the
velocities of the two bodies are inversely proportional to their
masses. Kinetic energy, however, is proportional to the square of the
velocities, and therefore the motion of the Moon carries about 81
times more kinetic energy than the motion of the Earth, around their
common center of gravity -- which lies inside the Earth, by the way,
so the Earth barely moves.
- Carol:
- Let me guess your next step. You want to compare the Earth-Moon
system with another system with an even larger mass ratio? Aha, I
see. Why not go all the way, and replace the Moon with a pebble,
orbiting the Earth at the same distance, but without the Moon being
there. The total mass is almost the same (we could even give the
Earth an extra percent of mass to preserve
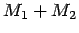 ), but clearly
the kinetic energy of the pebble is far far smaller than the kinetic
energy of the Moon. And using your argument, the pebble will still
carry almost all the kinetic energy of the Earth-pebble system, as did
the Moon before. The velocities of pebble and Moon are almost the same,
which means that for the whole system
), but clearly
the kinetic energy of the pebble is far far smaller than the kinetic
energy of the Moon. And using your argument, the pebble will still
carry almost all the kinetic energy of the Earth-pebble system, as did
the Moon before. The velocities of pebble and Moon are almost the same,
which means that for the whole system
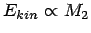 in the
limit where
in the
limit where 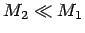 . Indeed, that is what
Eq. 3.4 tells us. Now I feel comfortable with
that result.
. Indeed, that is what
Eq. 3.4 tells us. Now I feel comfortable with
that result.
- Alice:
- If we continue like this, you'll both be turned into astronomers!
Yes, it is always a good idea to look at a new formula, and to think
of some limiting cases, to check whether the equation makes sense. Of
course, making sense does not really prove that the equation is correct.
We still have to check the derivation, which is given in many text books
on classical dynamics. However, we are at least guarded against most
typos, and more importantly, it gives us more of an idea of the
physics behind the mathematics.
- Bob:
- It is interesting that Eqs. 3.4,
3.5 have the exact same mass dependence, if we
switch back again to our notation in which
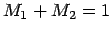 .
.
- Alice:
- Yes, and we can bring that out more clearly by introducing the notion
of what is called the `reduced mass'
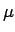 of a two-body system:
of a two-body system:
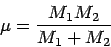 |
(3.6) |
- Carol:
- I see, if we define
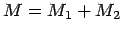 we then get:
we then get:
- Carol:
- Nice and elegant!
- Bob:
- Let me try to make it more elegant. I'm beginning to remember more
and more now from my physics class. There was this notion of specific
something as something per unit mass. How about defining those two
energy components as specific energies, per unit reduced mass? Let us
use a script
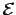 , rather than roman E, for that notion. In
our notation, with unit total mass, we will have the following
specific energies:
, rather than roman E, for that notion. In
our notation, with unit total mass, we will have the following
specific energies:
 |
(3.9) |
- Carol:
- So elegant and skinny that they almost disappear! But I suggest that
we keep calling those expressions simply kinetic and potential energy,
since we all know what we're talking about, rather than the mouthful
`specific kinetic and potential energy with respect to the reduced mass'.
- Alice:
- Agreed! Time to code it up.
- Carol:
- Does this look reasonable?
![\begin{Code}[forward\_euler4.C]
\small\verbatiminput{chap3/forward_euler4.C} \end{Code}](img212.png)
- Bob:
- Looks good to me. Let's start with our good old dt = 0.01

- Bob:
- Well, we knew that it was bad, and the energy check confirms it.
The energy even changes sign -- which of course we knew, since we saw
the particle escaping, and only positive-energy orbits can show escape.
- Carol:
- Rather than producing more output files, let's just confirm we have
the same output in this case, after which I suggest we call our friend
/dev/null to the rescue.

- Bob:
- Good! The same as before, with still the one step overshoot. Let's
look at the other cases.
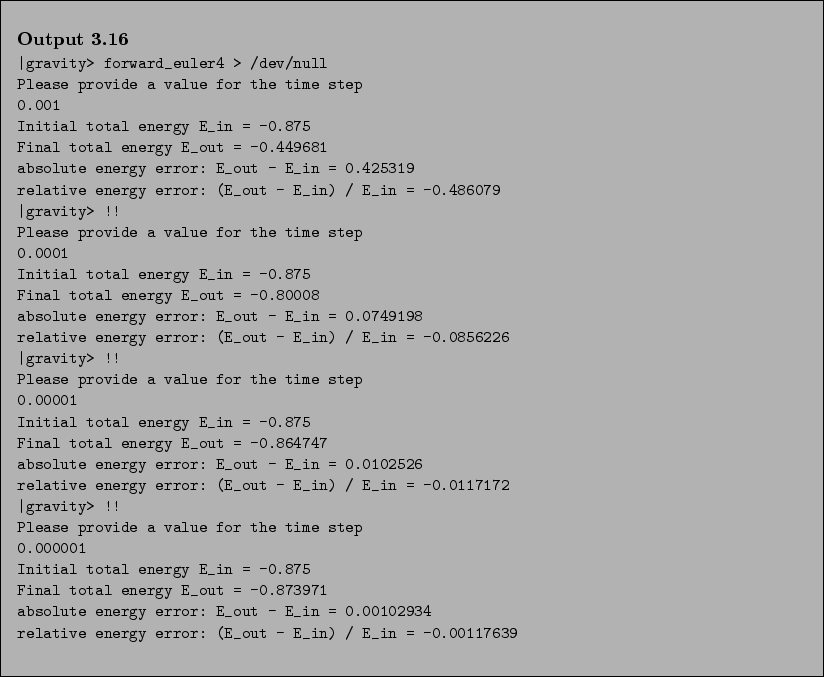
- Bob:
- How nice to see the errors shrink as snow for the sun!
- Carol:
- On a rather cold day, with a very low sun. Yes, it converges, but
very sloooooowly.
- Alice:
- I'm glad we went all the way to ten million steps, in the last
calculation, even though it took more than a minute to complete.
In the last two runs we have just confirmed the first-order character
of the forward Euler integration scheme. Making the time step ten
times smaller makes the error ten times smaller, to within the first
three significant digits! This is something that was not obvious at
all during the earlier runs, where the errors were so large that
nonlinear effects overwhelmed the asymptotic proportionality between
error and time step, for the limit
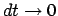 .
.
- Carol:
- Great! And a great point to stop. This has been a far longer session
than I had anticipated. Let's get back tomorrow, and then someone
else should take over the controls.
- Bob:
- I'd be happy to do so. This has been fun, and I look forward to
writing a second-order code.
- Alice:
- Happy dreams!




Next: 4. Exploring with a
Up: 3. Exploring with a
Previous: 3.6 Finding (slow) Convergence
The Art of Computational Science
2004/01/25