



Next: 5.5 Priming the Pump
Up: 5. Exploring with a
Previous: 5.3 Setting up Three
Let us follow the conversation of Alice, Bob, and Carol, while they
are using leapfrog2.C as a laboratory tool to investigate the
stability of the behavior of three bodies initially moving uniformly
and equally space along a circle. This time, Alice is behind the key
board.
- Alice:
- Having finally debugged our new 3-body leapfrog code enough to keep
the compiler happy, let us now see how the three stars behave when we
launch them on a circle. Here goes.
|gravity> g++ -o leapfrog2 leapfrog2.C
|gravity> leapfrog2 > leapfrog2_0.01_10.out
Please provide a value for the time step
0.01
and for the duration of the run
10
Initial total energy E_in = -0.866025
Final total energy E_out = -0.866025
absolute energy error: E_out - E_in = 2.72254e-10
relative energy error: (E_out - E_in) / E_in = -3.14372e-10
|gravity>
- Bob:
- Wow, what a small energy error! Clearly, our leapfrog code can run
circles around the forward Euler code.
- Alice:
- What you see here is partly an artifact of going around a perfect
circle. The leapfrog will do less well on an ellipse or on an
arbitrary orbit. The symmetry of the circle together with the time
symmetry of the leapfrog helps to cancels errors. So from the fact
that the energy errors are so small, I bet that we are still moving
happily around the initial circle.
- Carol:
- I don't want to bet yet, but let us inspect. Can you show us a
picture?
Figure 5.1:
The first attempt to integrate the orbits of three stars
starting off on a circle, with time step 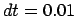 and a total
duration of
and a total
duration of 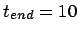
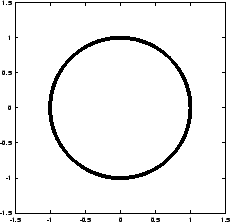 |
- Bob:
- You are right, Alice, as far as moving on a circle goes. Now I wonder
whether you were right about the stars developing an instability. It
doesn't look like it -- so far!
- Alice:
- Only one way to find out:
|gravity> leapfrog2 > leapfrog2_0.01_100.out
Please provide a value for the time step
0.01
and for the duration of the run
100
Initial total energy E_in = -0.866025
Final total energy E_out = -0.86602
absolute energy error: E_out - E_in = 5.63203e-06
relative energy error: (E_out - E_in) / E_in = -6.5033e-06
|gravity>
Figure 5.2:
The second attempt to integrate the orbits of three stars
starting off on a circle, with time step 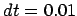 and a total
duration of
and a total
duration of 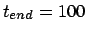
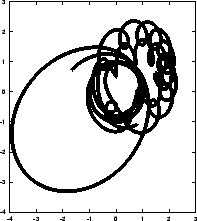 |
- Bob:
- Okay, Alice seems to be right on both counts! First of all, the
energy error is now ten thousand times larger, even though we ran only
ten times longer, so that confirms her circle argument. But before I
congratulate her on the instability, I have one nagging question.
I wonder whether this fancy three-body dance is caused by numerical
instabilities caused by finite accuracy of the leapfrog, or whether it
is a physical instability which real stars would undergo?
- Alice:
- I bet the latter, since we have not yet discovered even one such
system in the sky, even though we have found countless multiple stars,
from triples to quadruples and quintuples and up. But why don't we
check? Let's refine the time step a few times by an order of magnitude.
|gravity> leapfrog2 > leapfrog2_0.001_100.out
Please provide a value for the time step
0.001
and for the duration of the run
100
Initial total energy E_in = -0.866025
Final total energy E_out = -0.866025
absolute energy error: E_out - E_in = 1.58819e-07
relative energy error: (E_out - E_in) / E_in = -1.83388e-07
|gravity>
Figure 5.3:
The third attempt to integrate the orbits of three stars
starting off on a circle, with time step 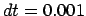 and a total
duration of
and a total
duration of 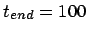
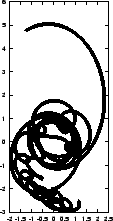 |
|gravity> leapfrog2 > leapfrog2_0.0001_100.out
Please provide a value for the time step
0.0001
and for the duration of the run
100
Initial total energy E_in = -0.866025
Final total energy E_out = -0.866025
absolute energy error: E_out - E_in = 1.1609e-09
relative energy error: (E_out - E_in) / E_in = -1.3405e-09
|gravity>
Figure 5.4:
The fourth attempt to integrate the orbits of three stars
starting off on a circle, with time step 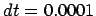 and a total
duration of
and a total
duration of 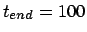
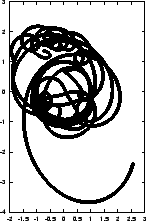 |
- Bob:
- Well, Alice, what did I tell you? Each picture is wildly different,
so I don't think that we are converging onto an actually existing
unstable orbit.
- Alice:
- Well, let's try one more refinement.
|gravity> leapfrog2 > leapfrog2_0.00001_100.out
Please provide a value for the time step
0.00001
and for the duration of the run
100
Initial total energy E_in = -0.866025
Final total energy E_out = -0.866025
absolute energy error: E_out - E_in = 1.17143e-10
relative energy error: (E_out - E_in) / E_in = -1.35265e-10
|gravity>
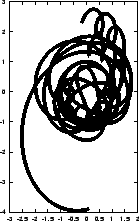
Figure 5.5:
The fifth attempt to integrate the orbits of three stars
starting off on a circle, with time step 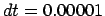 and a total
duration of
and a total
duration of 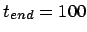
 |
- Alice:
- Well, at least the last two are somewhat similar, unlike all previous
pictures. But alike they are certainly not.
- Bob:
- Okay, one more refinement, and perhaps the whole thing will finally
converge! With dt = 0.000001, this means a hundred million steps,
but why not, computers are fast enough these days.
|gravity> leapfrog2 > leapfrog2_0.000001_100.out
Please provide a value for the time step
0.000001
and for the duration of the run
100
Initial total energy E_in = -0.866025
Final total energy E_out = -0.866025
absolute energy error: E_out - E_in = 8.68972e-13
relative energy error: (E_out - E_in) / E_in = -1.0034e-12
|gravity>
Figure 5.6:
The sixth attempt to integrate the orbits of three stars
starting off on a circle, with time step 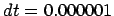 and a total
duration of
and a total
duration of 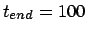
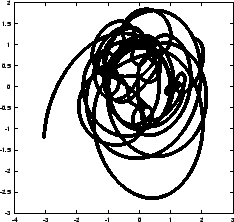 |
- Bob:
- So much for similar but not alike. This one doesn't look anything
like the previous one. And we are rapidly approaching machine accuracy.
- Alice:
- Hmmmm.




Next: 5.5 Priming the Pump
Up: 5. Exploring with a
Previous: 5.3 Setting up Three
The Art of Computational Science
2004/01/25






