With a better algorithm in hand, our friends decided to work their way
up from the two-body problem to the three-body problem. And rather
than hard coding the value of ![]() in their algorithm, they wrote a
leapfrog code for the general
in their algorithm, they wrote a
leapfrog code for the general ![]() -body problem. The expression for
the acceleration felt by particle
-body problem. The expression for
the acceleration felt by particle ![]() is given by summing together the
Newtonian gravitational attraction of all other particles
is given by summing together the
Newtonian gravitational attraction of all other particles ![]() , where
both
, where
both ![]() and
and ![]() take on values from 1 up to and including
take on values from 1 up to and including ![]() :
:
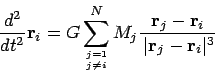 |
(5.1) |
Here ![]() and
and ![]() are the mass and position vector of particle
are the mass and position vector of particle ![]() ,
and
,
and ![]() is the gravitational constant. To bring out the inverse square
nature of gravity, we can define
is the gravitational constant. To bring out the inverse square
nature of gravity, we can define
![]() , with
, with
![]() , and unit vector
, and unit vector
![]() :
:
Note that the summation excludes self-interactions: every particle
feels the forces of the other ![]() particles, but not its own force
(which would be infinitely large in case of a point mass).
particles, but not its own force
(which would be infinitely large in case of a point mass).