



Next: 5.6 Reaching Convergence
Up: 5. Exploring with a
Previous: 5.4 Looking for Instabilities
- Carol:
- Hmmmm indeed. Aha! I have an idea. Even if the instability exists
in the real world, it still has to be triggered in some way. In our
computer it is triggered by round-off errors. In the real world, if
we put a pencil on its tip straight up and let go, the pencil will
fall in a random direction, triggered by the Brownian motion of the
air molecules, even if we had aligned it perfectly vertically.
Brownian motion is not reproducible, but neither can you expect
round-off errors to be reproducible when you change time steps.
- Alice:
- Interesting point! Let us try. Let us give one of the stars a little
perturbation in its velocity, on the order of
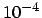 , huge compared
to the round-off noise around
, huge compared
to the round-off noise around 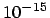 , but still larger than typical
numerical errors of the leapfrog, certainly for small enough step size.
Okay, here is a version, leapfrog2a.C. The only change I have
made with respect to leapfrog2a.C is the addition of one line,
immediately following the assignment of the velocities:
, but still larger than typical
numerical errors of the leapfrog, certainly for small enough step size.
Okay, here is a version, leapfrog2a.C. The only change I have
made with respect to leapfrog2a.C is the addition of one line,
immediately following the assignment of the velocities:
v[0][0] += 0.0001;
- Bob:
- I see. You are priming the pump, to guide the instability. And
you have put this line just after the velocity initialization,
so that it appears conveniently just before the first calculation of
the kinetic energy. That way, the first total energy calculation
takes this displacement in the value of this one velocity component
into account. By now, I do expect the system to fall apart again, and
I'm really curious. If the resulting dance pattern jumps all over the
place again, we definitely are dealing with errors introduced by the
leapfrog. But if we converge to one particular orbit, then I concede
that we have uncovered a physical instability, where a given
well-defined tiny displacement leads to a well-defined resulting way
in which the system falls apart. Let's have a look, Alice!
- Alice:
- I'll start again with only ten time units, to check that our
three stars complete at least a few orbits on their original circle,
before going their own way.
|gravity> g++ -o leapfrog2a leapfrog2a.C
|gravity> leapfrog2a > leapfrog2a_0.01_10.out
Please provide a value for the time step
0.01
and for the duration of the run
10
Initial total energy E_in = -0.866025
Final total energy E_out = -0.866025
absolute energy error: E_out - E_in = 1.21321e-09
relative energy error: (E_out - E_in) / E_in = -1.40089e-09
|gravity>
- Bob:
- Applying Alice's detective strategy, I would say that the energy error
is still too small to show detectable deviations from a circle.
Notice that the error is clearly larger than before, as we would
expect, since we have given the instability a hand by starting
with a gentle push.
- Alice:
- Elementary, my dear Bob. But let us see whether you are right.
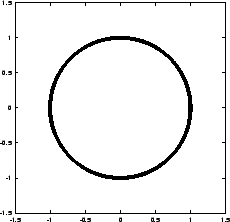
Figure 5.7:
The first attempt to integrate the orbits of three stars
starting off on a circle with an initial velocity perturbation of
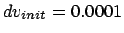 , time step
, time step 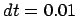 and a total duration of
and a total duration of
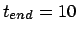
 |
- Bob:
- Encouraged by my success in following Alice's footsteps,, I will now
predict a significant degradation in the energy conservation, together
with the appearance of a wild three-body dance, when we go to 100 time
units.
- Alice:
- You should become my agent -- here are the run and the plot:
|gravity> leapfrog2a > leapfrog2a_0.01_100.out
Please provide a value for the time step
0.01
and for the duration of the run
100
Initial total energy E_in = -0.866025
Final total energy E_out = -0.865241
absolute energy error: E_out - E_in = 0.000784568
relative energy error: (E_out - E_in) / E_in = -0.000905941
|gravity>
Figure 5.8:
The second attempt to integrate the orbits of three stars
starting off on a circle with an initial velocity perturbation of
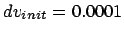 , time step
, time step 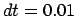 and a total duration of
and a total duration of
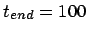
 |
- Carol:
- I bet Bob didn't envision such a big degradation in energy
conservation! Let's make the time steps a factor ten smaller.
|gravity> leapfrog2a > leapfrog2a_0.001_100.out
Please provide a value for the time step
0.001
and for the duration of the run
100
Initial total energy E_in = -0.866025
Final total energy E_out = -0.866033
absolute energy error: E_out - E_in = -7.29447e-06
relative energy error: (E_out - E_in) / E_in = 8.42293e-06
|gravity>
Figure 5.9:
The third attempt to integrate the orbits of three stars
starting off on a circle with an initial velocity perturbation of
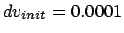 , time step
, time step 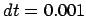 and a total duration of
and a total duration of
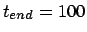
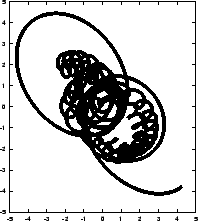 |
- Bob:
- You are right, I had expected an energy error more like the present
one, already in the previous round.
- Alice:
- My hunch is that the previous round may have featured a particularly
close encounter. Since our code does not know how to decrease the
time step during close encounters, even one such encounter can spoil
the energy conservation of a whole run. At some point we'll have to
make our integrator smarter and more autonomous in the eye of danger.
- Carol:
- But not now. I want to see whether we will reach convergence. So far
the last two pictures don't look any more like each other than in the
case before we primed the pump. Can we refine the time step by
another order of magnitude?
- Alice:
- Sure, my pleasure.




Next: 5.6 Reaching Convergence
Up: 5. Exploring with a
Previous: 5.4 Looking for Instabilities
The Art of Computational Science
2004/01/25


