5.8 Three Bodies on a Figure Eight

The next time Alice, Bob, and Carol met, they decided to make one more modification to their 3-body version of the leapfrog code, before going to a more modular and flexible $N$-body version. Alice had mentioned a relatively recent discovery of a new solution to the centuries old three-body problem, in the form of three stars of equal mass following each other along a single orbit resembling a figure eight. Here is the first half of the code, which lists the initial conditions, followed by the computation of the initial accelerations as well as kinetic and potential energy. The second half of the code is identical to the second half of leapfrog2.C.

They first tried their standard time step choice dt = 0.01 for a integration until t_end = 100:

|gravity> g++ -o leapfrog3 leapfrog3.C
|gravity> leapfrog3 > leapfrog3_0.01_100.out
Please provide a value for the time step
0.01
and for the duration of the run
100
Initial total energy E_in = -1.28705
Final total energy E_out = -1.28706
absolute energy error: E_out - E_in = -1.25936e-05
relative energy error: (E_out - E_in) / E_in = 9.78486e-06
|gravity>

Figure 5.13: The first attempt to integrate the orbits of three stars starting off on a figure-8 orbit with time step $dt = 0.01$ and a total duration of $t_{end} = 100$

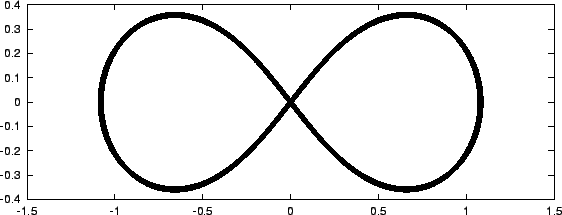Even though the energy error was not that small, no deviation in the orbit was visible. Clearly, the three-body figure-8 orbit is far more stable than the three-body circular orbit, which fell apart well before reaching 100 time units, as we saw before. Taking a ten times smaller time step neatly decreased the errors by a factor of one hundred, also a good sign of reaching convergence in the orbits:

|gravity> leapfrog3 > leapfrog3_0.001_100.out
Please provide a value for the time step
0.001
and for the duration of the run
100
Initial total energy E_in = -1.28705
Final total energy E_out = -1.28705
absolute energy error: E_out - E_in = -1.19725e-07
relative energy error: (E_out - E_in) / E_in = 9.30233e-08
|gravity>

When plotting this last result, it looks exactly like Fig. 5.13, so we will omit it here.

Our friends then repeated the second test for instability, by `priming the pump' again, with an offset of $10^{-4}$ in the $x$ component of the first particle. As before, they added the one line

    v[0][0] += 0.0001;

immediately following the assignment of velocities at the beginning of the program. They renamed this modified code leapfrog3a.C. Here is what happened by t_end = 100:

|gravity> g++ -o leapfrog3a leapfrog3a.C
|gravity> leapfrog3a > leapfrog3a_0.001_100.out
Please provide a value for the time step
0.001
and for the duration of the run
100
Initial total energy E_in = -1.287
Final total energy E_out = -1.287
absolute energy error: E_out - E_in = -1.27819e-07
relative energy error: (E_out - E_in) / E_in = 9.93155e-08
|gravity>

Figure 5.14: The first attempt to integrate the orbits of three stars starting off on a figure-8 orbit with an initial velocity perturbation of $dv_{init}=0.0001$, time step $dt = 0.001$ and a total duration of $t_{end} = 100$

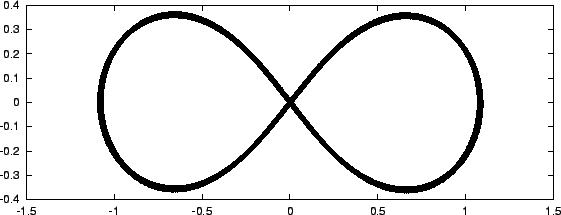Again, no visible deviations, very similar small energy errors, and no sign of any instability. This confirms what has been described in the literature, that the figure-8 orbit for three bodies is stable.

We leave it as an exercise for the reader to explore when and how the figure-8 configuration falls apart (or perhaps winds up in a higher order version of a stable orbit, with more loops and turns) upon an increase of the magnitude of the perturbation, either in one of the velocity components or in one of the position components, or in a mix of perturbations of various position and velocity components.