6.1 A Surprisingly Simple Hermite Scheme

The most symmetric Hermite version, and the one closest resembling the leapfrog is this one:

$${\bf r}_{i+1} = {\bf r}_i + {\textstyle\frac{1}{2}}({\bf v}_i + {\bf v}_{i+1}) dt + {\textstyle\frac{1}{12}}({\bf a}_i - {\bf a}_{i+1})(dt)^2$$ (6.1)

$${\bf v}_{i+1} = {\bf v}_i + {\textstyle\frac{1}{2}}({\bf a}_i + {\bf a}_{i+1}) dt + {\textstyle\frac{1}{12}}({\bf j}_i - {\bf j}_{i+1})(dt)^2$$ (6.2)

Here ${\bf j}= d{\bf a}/dt$ is the jerk, the time derivative of the acceleration, and therefore the third time derivative of position:

$${\bf j}= \frac{d^3}{dt^3} {\bf r}$$ (6.3)

The term `jerk' has crept into the literature relatively recently, probably originally as a pun. If a car or train changes acceleration relatively quickly you experience not a smoothly accelerating or decelerating motion, but instead a rather `jerky' one.

The jerk can be computed through straightforward differentiation of Newton's gravitational equations, Eq. 5.2:

$${\bf j}_i = G \sum_{j=1 \atop j \neq i}^N \,M_j \left[ \frac... ...({\bf r}_{ji}\cdot{\bf v}_{ji}){\bf r}_{ji}}{r_{ji}^5} \right]$$ (6.4)

where ${\bf v}_{ji} = {\bf v}_j - {\bf v}_i$.

As an aside, note that the jerk has one very convenient property. Although the expression above looks quite a bit more complicated than Newton's original equations, they can still be evaluated through one pass over the whole $N$-body system. This is no longer true for higher derivatives. For example, we can obtain the fourth derivative of the position of particle $i$ (the snap, see next section) by differentiating Eq. 6.4:

$$\frac{d^4}{dt^4}{\bf r}_i = G \sum_{j=1 \atop j \neq i}^N \,M_j \Bigg[ \, \frac{{\bf a}_{ji}}{r_{ji}^3} -6 \frac{({\bf r}_{ji}\cdot{\bf v}_{ji})}{r_{ji}^5}{\bf v}_{ji}$$

$$\, + \left\{ -3\frac{v_{ji}^2}{r_{ji}^5} -3 \frac{({\bf r}_{ji}\cdot... ...c{({\bf r}_{ji}\cdot{\bf v}_{ji})^2}{r_{ji}^7} \right\} {\bf r}_{ji} \,\,\Bigg]$$ (6.5)

where ${\bf a}_{ji} = {\bf a}_j - {\bf a}_i$, and this is the expression that thickens the plot. Unlike the ${\bf r}_{ji}$ and ${\bf v}_{ji}$ expressions, that are given by the initial conditions, ${\bf a}_{ji}$ has to be calculated from the positions and velocities. However, this calculation does not only involve the pairwise attraction of particle $j$ on particle $i$, but in fact all pairwise attractions of all particles on each other! This follows immediately when we write out what the shorthand implies:

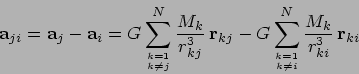$${\bf a}_{ji} = {\bf a}_j - {\bf a}_i = G \sum_{k=1 \atop k \... ...sum_{k=1 \atop k \neq i}^N \frac{M_k}{r_{ki}^3} \,{\bf r}_{ki}$$ (6.6)

When we substitute this back into Eq. 6.5, we see that we have to do a double pass over the $N$-body system, summing over both indices $k$ and $j$ in order to compute a single fourth derivative for the position of particle $i$.