



Next: 10. A 25-body Example
Up: 9. Setting up a
Previous: 9.3 Testing, testing, .
- Bob:
- Well, the one part which I must admit I did not fully understand is
where the angles are used to create particle positions in, what did
you call it again?
- Alice:
- spherical coordinates. A useful way to label particles by their
distance from the center, and by the two angles needed in addition to
locate them uniquely.
- Carol:
- Useful, yes, if they do what they are supposed to do. Bob may be right,
that is a likely place to have made a mistake. Let us look at how
exactly we made that transformation. Here is how we assigned the
positions and velocities to all the particles.
![\begin{Code}[sphere1a\_bugfragment.C: put\_snapshot]
\small\verbatiminput{chap9/sphere1a_bugfragment.C} \end{Code}](img756.png)
- Alice:
- At first sight, it looks rather reasonable. I clearly recognize the
spherical coordinate angles in the position assignments: the sines and
cosines of
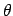 and
and 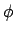 are all in the right place.
are all in the right place.
- Carol:
- And the ranges above those three lines are correct too:
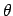 moves
from the north pole to the south pole, so to speak, which makes an arc
of
moves
from the north pole to the south pole, so to speak, which makes an arc
of 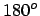 , starting at
, starting at 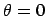 , as it should; similarly
, as it should; similarly 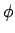 moves all the way around along the equator, describing an angle of
moves all the way around along the equator, describing an angle of 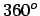 .
What could possibly be wrong?
.
What could possibly be wrong?
- Bob:
- Why are the
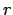 values distributed according to a one-third power?
values distributed according to a one-third power?
- Alice:
- That's because the size of a volume element increases with the cube of
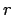 .
For example, if you double the radius of a three-dimensional object,
you make the volume eight times large. In order to keep the same
density of points, you have to put eight times as many particles.
.
For example, if you double the radius of a three-dimensional object,
you make the volume eight times large. In order to keep the same
density of points, you have to put eight times as many particles.
- Bob:
- I see. You want to distribute the particles uniformly random in
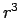 ,
not in
,
not in 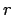 . So this means that
. So this means that 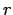 , which is the third root of
, which is the third root of 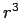 ,
has to follow the third root of a uniformly distributed variable.
,
has to follow the third root of a uniformly distributed variable.
- Alice:
- You got it.
- Bob:
- And the angles don't need such a trick, because
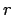 does not change
while we move around the latitude
does not change
while we move around the latitude 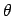 or the longitude
or the longitude 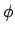 .
.
- Alice:
- Right you are, that is indeed ...OOPS ...no ...correction ...
that is not indeed right, that is wrong. Now I see our mistake!
- Carol:
- But look, if you go around the equator, how can it make any difference
to where on the equator you are?
- Alice:
- It doesn't, but try going to one of the poles.
- Carol:
- Ah, now I get it. Moving from the equator to the pole, the lines of
constant longitude converge together, and there is less and less room
between them, the closer you get to the pole.
- Alice:
- And mathematically you express that by the expression for a volume
element
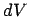 as:
as:
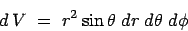 |
(9.1) |
- Alice:
- And for our application, it is easier to write this as
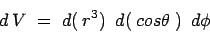 |
(9.2) |
- Bob:
- So this means that we have to invert the cosine factor for
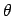 ,
just as we inverted the third power for
,
just as we inverted the third power for 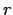 in the line above in our
code.
in the line above in our
code.
- Alice:
- Exactly. And the inverse of `
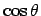 ' is `
' is `
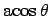 ,
sometimes also written as `
,
sometimes also written as `
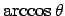 .' If we
sprinkle particles along latitude in such a way that we do it as the
arc cosine of
.' If we
sprinkle particles along latitude in such a way that we do it as the
arc cosine of 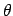 , we will no longer overpopulate the poles.
, we will no longer overpopulate the poles.
- Carol:
- Ah, so that is what cause the crowding at the poles, something that
showed up only in the
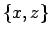 plot.
plot.
- Bob:
- Because in the
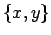 plot the poles are projected in the middle of
the equatorial plane. The bug was less obvious there, although it did
create the spike in the center, which we all overlooked in the first
figure, which was a bit crowded with
plot the poles are projected in the middle of
the equatorial plane. The bug was less obvious there, although it did
create the spike in the center, which we all overlooked in the first
figure, which was a bit crowded with 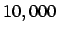 particles.
particles.
- Alice:
- Well, I'm really glad we have found the bug, and it is easy to fix.
Let us call the corrected code sphere1.C. The only difference
is the line for assigning random number values to
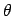 :
:
|gravity> diff sphere1.C sphere1a.C
197c197
< real theta = acos(randinter(-1.0, 1.0));
---
> real theta = randinter(0.0, PI);
|gravity>
\cba
\abc
\carol
Let's see whether things come out better.
\cba
\begin{small}
\begin{verbatim}
|gravity> sphere1 -n 1000 | tail +3 > test1_1000.out
seed = 1063988487
|gravity> gnuplot
Terminal type set to 'x11'
gnuplot> plot "test1_1000.out" using 2:3 notitle
gnuplot>
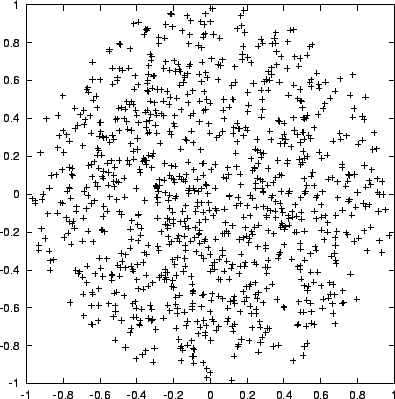
Figure:
Output of sphere1, with 1,000 particles, projected onto the
 plane
plane
 |
- Bob:
- (fig. 9.5)
What a difference a line of code can make! No spike in the center any
more. Everything looks so much smoother.
- Carol:
- Indeed. There is only a mild edge effect, with somewhat fewer
particles far away from the center, but the contrast between center
and edge is much less than it was before.
- Alice:
- This suggest that our central vertical line has cleared away. Let's
make sure.
|gravity> gnuplot
Terminal type set to 'x11'
gnuplot> plot "test1_1000.out" using 2:4 notitle
gnuplot>
Figure:
Output of sphere1, with 1,000 particles, projected onto the
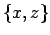 plane
plane
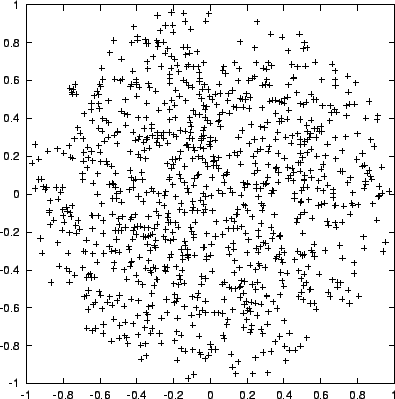 |
- Bob:
- (fig. 9.6)
Indeed, a clean bill of health for sphere1.C
- Carol:
- The moral of the story seems to be to try to test each module before
you start putting things together, no matter how tempting it is to
quickly write a few pieces and do some fun experiment with it.
- Bob:
- Yes, and this must be equally true for real experiments as well as for
virtual experiments in cyberspace. This reminds me of what I just
heard from a friend of mine, a graduate student in physics. He talked
about an experiment he was involved in. The wanted to test a new
magnet, to be used to deflect a particle beam, in his case a beam of
polarized electrons. After finishing the construction of the magnet
setup, they bought a standard device that produced polarized electrons
of the right type, hooked it up to the magnet, and switched everything
on. If all had gone well, fine, but in their case things did not go
well. The result is not what they expected, and they didn't know at
that point whether there was something wrong with the magnet, with the
gadget producing the electrons, with the connection between the two
devices, or with the apparatus reading out the results (or even with
the operator of the equipment who might have had a bad day and
therefore made some kind of mistake).
- Alice:
- It would have been worse, much worse actually, if all had seemed
fine at first, but only because some subtle bug in one of the devices
produced an error that happened to be canceled more or less by another
error in another part of the setup.
- Bob:
- That was his conclusion too. He told me he realized that it is
crucially important to test one by one all the steps in constructing an
experimental setup. The first step should have been to make sure that
the gadget generating the electrons is really doing what they expected
and hoped it would do. In other words, they should first have carefully
measured the properties of the electron beam before it entered
the magnet setup. Only when they really felt comfortable that their
gadget was working as advertised would it make sense to connect
it to the magnet, and to start analyzing the beam coming out of the
magnet.
- Carol:
- I think the analogy is a good one, and that what is true for a
traditional lab is true for our virtual lab as well. We did not
really confront this problem earlier, since we dealt only with two or
three particles, for which we wrote the initial conditions by hand. In
contrast, we now have reached a point where for the first time we are
generating initial conditions automatically. And anything that is
done automatically can go wrong in all kind of unexpected ways.
- Alice:
- Well, it is still possible to make mistakes when entering numbers
by hand. I sure have done that more often than I'd like to admit.
- Carol:
- Of course, but when you are dealing with a two-body or three-body
system, you can track the orbits individually on the screen, and if
you are careful, you will notice if the particles behave completely
different from what you expected. But as soon as we start generating
initial conditions automatically in large numbers, for a 25-body
system for example, the situation is drastically different. It is no
longer possible to look at the spaghetti of tangled orbits on a screen
and to decide whether all 25 particles do even remotely what they are
supposed to do. And indeed, the whole reason to use a computer,
rather than pen and paper, is to solve a problem that is too complex
to predict analytically beforehand. So you don't know in detail
what to expect, and you may not notice if any part of the system
behaves differently from how it should behave.
- Bob:
- I bet your must have heard about modular testing in one of your
computer science classes.
- Carol:
- Yes, but frankly I thought they exaggerated a bit. The typical home
work problems were often so simple that it was easy to see whether
you got it right or not. But with our example today, I can see how
essential it is to test each and every module you write, before
hooking it up to other modules. If you test modules one by one, then
it is most likely that a new bug in a complex of modules is generated
by the latest module you have just added; or at least is caused by an
unexpected interaction between that new module and what was already
tested before. In both cases, you are far better off than if you
suddenly have to test a whole conglomeration of modules, where errors
could be hidden in any of them.
- Alice:
- That last scenario is a nightmare, and a good way to quickly loose
interest in computer programming.
Exercise 9.1 (Rejection technique)
Inspect the following code. It uses a completely different technique
to generate initial conditions for a homogeneous sphere. It is
simpler in that it does not use any trigonometric functions, but only
the usual Cartesian coordinates. This sounds almost too good to be
true. Can you figure out how the rejection technique works? Try it
out and compare its results with that of
sphere1.C.
![\begin{Code}[sphere2.C]
\small\verbatiminput{chap9/sphere2.C} \end{Code}](img790.png)




Next: 10. A 25-body Example
Up: 9. Setting up a
Previous: 9.3 Testing, testing, .
The Art of Computational Science
2004/01/25
![\begin{Code}[sphere1a\_bugfragment.C: put\_snapshot]
\small\verbatiminput{chap9/sphere1a_bugfragment.C} \end{Code}](img756.png)